Menu Close

Question-113682

Tinku Tara 0 Comments
Pin




Question Number 113682 by mohammad17 last updated on 14/Sep/20
Commented by mohammad17 last updated on 14/Sep/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 14/Sep/20
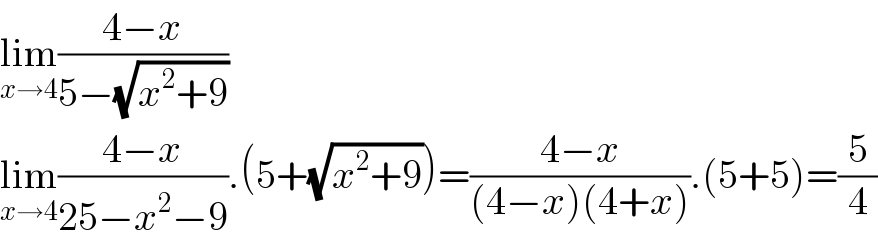
lim_(x→4) ((4−x)/(5−(√(x^2 +9)))) lim_(x→4) ((4−x)/(25−x^2 −9)).(5+(√(x^2 +9)))=((4−x)/((4−x)(4+x))).(5+5)=(5/4)
$$\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\frac{\mathrm{4}−{x}}{\mathrm{5}−\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}} \\ $$$$\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\frac{\mathrm{4}−{x}}{\mathrm{25}−{x}^{\mathrm{2}} −\mathrm{9}}.\left(\mathrm{5}+\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\right)=\frac{\mathrm{4}−{x}}{\left(\mathrm{4}−{x}\right)\left(\mathrm{4}+{x}\right)}.\left(\mathrm{5}+\mathrm{5}\right)=\frac{\mathrm{5}}{\mathrm{4}} \\ $$
Commented by mohammad17 last updated on 15/Sep/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 14/Sep/20
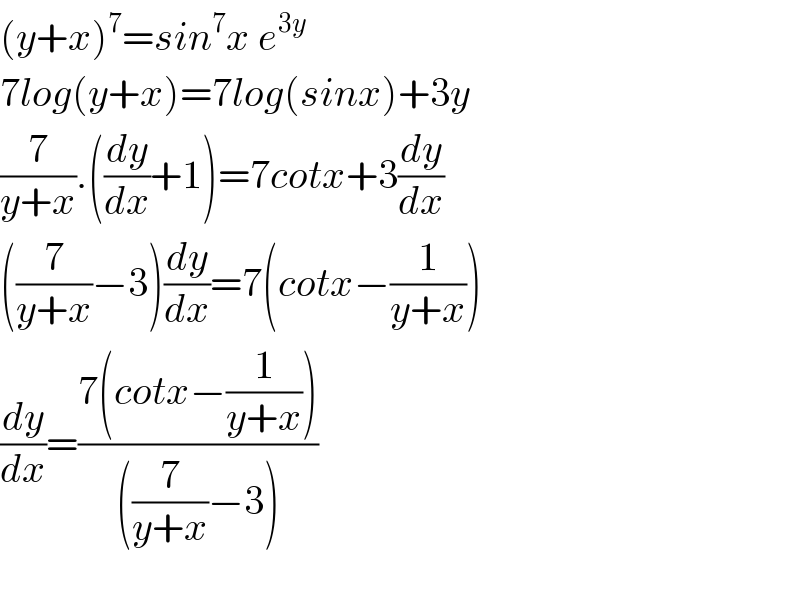
(y+x)^7 =sin^7 x e^(3y) 7log(y+x)=7log(sinx)+3y (7/(y+x)).((dy/dx)+1)=7cotx+3(dy/dx) ((7/(y+x))−3)(dy/dx)=7(cotx−(1/(y+x))) (dy/dx)=((7(cotx−(1/(y+x))))/(((7/(y+x))−3)))
$$\left({y}+{x}\right)^{\mathrm{7}} ={sin}^{\mathrm{7}} {x}\:{e}^{\mathrm{3}{y}} \\ $$$$\mathrm{7}{log}\left({y}+{x}\right)=\mathrm{7}{log}\left({sinx}\right)+\mathrm{3}{y} \\ $$$$\frac{\mathrm{7}}{{y}+{x}}.\left(\frac{{dy}}{{dx}}+\mathrm{1}\right)=\mathrm{7}{cotx}+\mathrm{3}\frac{{dy}}{{dx}} \\ $$$$\left(\frac{\mathrm{7}}{{y}+{x}}−\mathrm{3}\right)\frac{{dy}}{{dx}}=\mathrm{7}\left({cotx}−\frac{\mathrm{1}}{{y}+{x}}\right) \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{7}\left({cotx}−\frac{\mathrm{1}}{{y}+{x}}\right)}{\left(\frac{\mathrm{7}}{{y}+{x}}−\mathrm{3}\right)} \\ $$$$ \\ $$
Commented by mohammad17 last updated on 15/Sep/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by Mr.D.N. last updated on 14/Sep/20
A) Prove that cos^2 θ+sin^2 θ=1 Sol^n : We know, trigonometric ratio: sinθ = (p/h) and cos θ= (b/h) or, p= h sinθ and b= h cosθ We know Pythagorous theorem, p^2 +b^2 =h^2 or, (h sinθ)^2 +(h cosθ)^2 = h^2 or,h^2 sin^2 θ +h^2 cos^2 θ = h^2 or, h^2 (sin^2 θ + cos^2 θ) = h^2 or, sin^2 θ + cos^2 θ = (h^2 /h^2 ) ∴ sin^2 θ + cos^2 θ = 1 which is required proof.
$$\: \\ $$$$\left.\:\mathrm{A}\right)\:\mathrm{Prove}\:\mathrm{that}\:\:\:\:\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta=\mathrm{1} \\ $$$$\:\:\mathrm{Sol}^{\mathrm{n}} :\:\: \\ $$$$\:\mathrm{We}\:\mathrm{know},\:\mathrm{trigonometric}\:\mathrm{ratio}: \\ $$$$\:\:\mathrm{sin}\theta\:=\:\frac{\mathrm{p}}{\mathrm{h}}\:\:\mathrm{and}\:\mathrm{cos}\:\theta=\:\frac{\mathrm{b}}{\mathrm{h}}\: \\ $$$$\:\mathrm{or},\:\mathrm{p}=\:\mathrm{h}\:\mathrm{sin}\theta\:\:\:\:\mathrm{and}\:\:\mathrm{b}=\:\mathrm{h}\:\mathrm{cos}\theta \\ $$$$\:\mathrm{We}\:\mathrm{know}\:\mathrm{Pythagorous}\:\mathrm{theorem}, \\ $$$$\:\:\:\:\mathrm{p}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{h}^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{or},\:\:\:\left(\mathrm{h}\:\mathrm{sin}\theta\right)^{\mathrm{2}} +\left(\mathrm{h}\:\mathrm{cos}\theta\right)^{\mathrm{2}} =\:\mathrm{h}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{or},\mathrm{h}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \theta\:+\mathrm{h}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \theta\:=\:\mathrm{h}^{\mathrm{2}} \\ $$$$\:\:\:\mathrm{or},\:\:\mathrm{h}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \theta\:+\:\mathrm{cos}^{\mathrm{2}} \theta\right)\:=\:\mathrm{h}^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{or},\:\:\mathrm{sin}^{\mathrm{2}} \theta\:+\:\mathrm{cos}^{\mathrm{2}} \theta\:\:=\:\frac{\mathrm{h}^{\mathrm{2}} }{\mathrm{h}^{\mathrm{2}} } \\ $$$$\:\:\:\therefore\:\:\mathrm{sin}^{\mathrm{2}} \theta\:+\:\mathrm{cos}^{\mathrm{2}} \theta\:=\:\mathrm{1}\:\:\:\:\mathrm{which}\:\mathrm{is}\:\mathrm{required}\:\mathrm{proof}. \\ $$$$\: \\ $$$$ \\ $$
Commented by mohammad17 last updated on 15/Sep/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by Mr.D.N. last updated on 14/Sep/20
Q5 1− By using first principle derivative prove that the derivative of tan x = sec^2 x Sol^n : We first principle derivative rules : f^( ′) (x) = _(h→0) ^(lim) ((f(x+h)−f(x))/h) Let, f(x) = tan x f(x+h)= tan(x+h) (d/dx) (tan x) = _(h→0) ^( lim) ((tan(x+h)−tan x)/h) = _(h→0) ^(lim) (( ((sin(x+h))/(cos(x+h))) −((sin x)/(cos x)))/h) = _(h→0) ^(lim) (((cos x sin(x+h)−sinx cos(x+h))/(cos x cos(x+h)))/h) = _(h→0) ^(lim) ((cos x (sin x cos h+cosx sin h)−sinx(cos x cos h−sinx sin h))/(h cos x cos(x+h))) = _(h→0) ^(lim) ((cos x sin x cos h + cos^2 x sin h−sin x cos x cos h +sin^2 x sin h)/(h cos x cos(x+h))) = _(h→0) ^(lim) ((cos^2 x sin h + sin^2 x sin h)/(h cos x cos(x+h))) = _(h→0) ^(lim) ((sin h (cos^2 x+sin^2 x))/(h cos x cos(x+h))) { ∵ sin^2 x+cos^2 x=1} = _(h→0) ^(lim) ((sin h)/h) × _(h→0) ^(lim) (1/(cos x cos(x+h))) { ∵ _(h→0) ^(lim) ((sin h)/h)=1} = 1× (1/(cos x .cos(x+0))) = (1/(cos x .cos x))= (1/(cos^2 x)) = sec^2 x ∴ (d/dx) ( tan x ) = sec^2 x proved//.
$$\:\mathrm{Q5} \\ $$$$\:\mathrm{1}−\:\mathrm{By}\:\mathrm{using}\:\mathrm{first}\:\mathrm{principle}\:\mathrm{derivative}\:\mathrm{prove} \\ $$$$\:\:\mathrm{that}\:\mathrm{the}\:\mathrm{derivative}\:\mathrm{of} \\ $$$$\:\:\mathrm{tan}\:\mathrm{x}\:=\:\mathrm{sec}^{\mathrm{2}} \mathrm{x} \\ $$$$\:\:\:\mathrm{Sol}^{\mathrm{n}} :\:\:\: \\ $$$$\:\:\:\mathrm{We}\:\mathrm{first}\:\mathrm{principle}\:\mathrm{derivative}\:\mathrm{rules}\:: \\ $$$$\:\:\:\mathrm{f}^{\:'} \:\left(\mathrm{x}\right)\:=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\frac{\mathrm{f}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{h}} \\ $$$$\:\mathrm{Let},\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{tan}\:\mathrm{x} \\ $$$$\:\:\mathrm{f}\left(\mathrm{x}+\mathrm{h}\right)=\:\mathrm{tan}\left(\mathrm{x}+\mathrm{h}\right) \\ $$$$\:\:\:\:\frac{\mathrm{d}}{\mathrm{dx}}\:\left(\mathrm{tan}\:\mathrm{x}\right)\:=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\:\mathrm{lim}} {\:}}\:\:\frac{\mathrm{tan}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{tan}\:\mathrm{x}}{\mathrm{h}} \\ $$$$\:\:\:\:=\:\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\frac{\:\frac{\mathrm{sin}\left(\mathrm{x}+\mathrm{h}\right)}{\mathrm{cos}\left(\mathrm{x}+\mathrm{h}\right)}\:−\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}}{\mathrm{h}} \\ $$$$\:\:\:=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\:\frac{\frac{\mathrm{cos}\:\mathrm{x}\:\mathrm{sin}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{sinx}\:\mathrm{cos}\left(\mathrm{x}+\mathrm{h}\right)}{\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\left(\mathrm{x}+\mathrm{h}\right)}}{\mathrm{h}} \\ $$$$\:\:=\underset{\boldsymbol{\mathrm{h}}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\:\frac{\mathrm{cos}\:\mathrm{x}\:\left(\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{h}+\mathrm{cosx}\:\mathrm{sin}\:\mathrm{h}\right)−\mathrm{sinx}\left(\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{h}−\mathrm{sinx}\:\mathrm{sin}\:\mathrm{h}\right)}{\mathrm{h}\:\mathrm{cos}\:\mathrm{x}\:\:\mathrm{cos}\left(\mathrm{x}+\mathrm{h}\right)} \\ $$$$\:=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\frac{\mathrm{cos}\:\mathrm{x}\:\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{h}\:+\:\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}\:\mathrm{h}−\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{h}\:+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}\:\mathrm{h}}{\mathrm{h}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\left(\mathrm{x}+\mathrm{h}\right)} \\ $$$$\:\:\:\:=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}\:\mathrm{h}\:+\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}\:\mathrm{h}}{\mathrm{h}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\left(\mathrm{x}+\mathrm{h}\right)} \\ $$$$\:\:=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\:\frac{\mathrm{sin}\:\mathrm{h}\:\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{h}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\left(\mathrm{x}+\mathrm{h}\right)}\:\:\:\:\:\:\:\:\:\:\:\left\{\:\because\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}=\mathrm{1}\right\} \\ $$$$\:\:=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\:\:\frac{\mathrm{sin}\:\mathrm{h}}{\mathrm{h}}\:\:×\:\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\left(\mathrm{x}+\mathrm{h}\right)}\:\:\:\:\:\:\left\{\:\because\underset{\mathrm{h}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\frac{\mathrm{sin}\:\mathrm{h}}{\mathrm{h}}=\mathrm{1}\right\} \\ $$$$\:=\:\:\mathrm{1}×\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}\:.\mathrm{cos}\left(\mathrm{x}+\mathrm{0}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}\:.\mathrm{cos}\:\mathrm{x}}=\:\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:=\:\mathrm{sec}^{\mathrm{2}} \mathrm{x} \\ $$$$\:\:\:\therefore\:\:\frac{\mathrm{d}}{\mathrm{dx}}\:\left(\:\mathrm{tan}\:\mathrm{x}\:\right)\:=\:\mathrm{sec}^{\mathrm{2}} \mathrm{x}\:\:\:\:\:\mathrm{proved}//. \\ $$
Commented by mohammad17 last updated on 15/Sep/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by Mr.D.N. last updated on 14/Sep/20
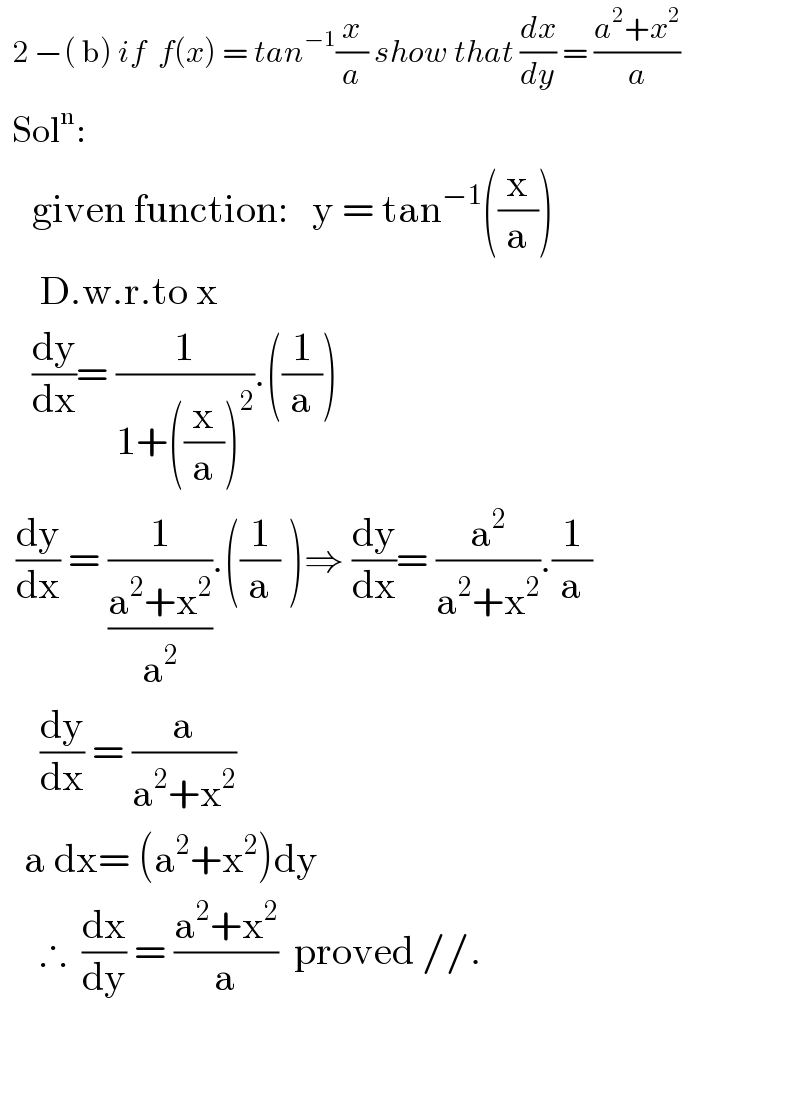
2 −( b) if f(x) = tan^(−1) (x/a) show that (dx/dy) = ((a^2 +x^2 )/a) Sol^n : given function: y = tan^(−1) ((x/a)) D.w.r.to x (dy/dx)= (1/(1+((x/a))^2 )).((1/a)) (dy/dx) = (1/((a^2 +x^2 )/a^2 )).((1/a) )⇒ (dy/dx)= (a^2 /(a^2 +x^2 )).(1/a) (dy/dx) = (a/(a^2 +x^2 )) a dx= (a^2 +x^2 )dy ∴ (dx/dy) = ((a^2 +x^2 )/a) proved //.
$$\:\:\mathrm{2}\:−\left(\:\mathrm{b}\right)\:{if}\:\:{f}\left({x}\right)\:=\:{tan}^{−\mathrm{1}} \frac{{x}}{{a}}\:{show}\:{that}\:\frac{{dx}}{{dy}}\:=\:\frac{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }{{a}}\:\:\: \\ $$$$\:\:\mathrm{Sol}^{\mathrm{n}} : \\ $$$$\:\:\:\:\mathrm{given}\:\mathrm{function}:\:\:\:\mathrm{y}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{a}}\right) \\ $$$$\:\:\:\:\:\mathrm{D}.\mathrm{w}.\mathrm{r}.\mathrm{to}\:\mathrm{x} \\ $$$$\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\:\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{\mathrm{x}}{\mathrm{a}}\right)^{\mathrm{2}} }.\left(\frac{\mathrm{1}}{\mathrm{a}}\right) \\ $$$$\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{1}}{\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}.\left(\frac{\mathrm{1}}{\mathrm{a}}\:\right)\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}=\:\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }.\frac{\mathrm{1}}{\mathrm{a}} \\ $$$$\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\:\:\mathrm{a}\:\mathrm{dx}=\:\left(\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right)\mathrm{dy} \\ $$$$\:\:\:\:\:\therefore\:\:\frac{\mathrm{dx}}{\mathrm{dy}}\:=\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }{\mathrm{a}}\:\:\mathrm{proved}\://. \\ $$$$ \\ $$$$ \\ $$
Commented by mohammad17 last updated on 15/Sep/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 14/Sep/20
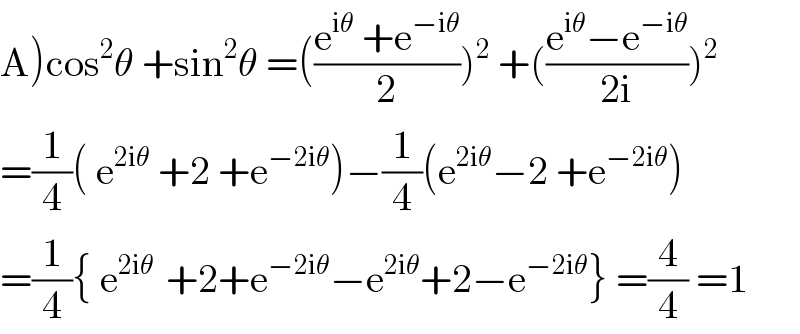
A)cos^2 θ +sin^2 θ =(((e^(iθ) +e^(−iθ) )/2))^2 +(((e^(iθ) −e^(−iθ) )/(2i)))^2 =(1/4)( e^(2iθ) +2 +e^(−2iθ) )−(1/4)(e^(2iθ) −2 +e^(−2iθ) ) =(1/4){ e^(2iθ ) +2+e^(−2iθ) −e^(2iθ) +2−e^(−2iθ) } =(4/4) =1
$$\left.\mathrm{A}\right)\mathrm{cos}^{\mathrm{2}} \theta\:+\mathrm{sin}^{\mathrm{2}} \theta\:=\left(\frac{\mathrm{e}^{\mathrm{i}\theta} \:+\mathrm{e}^{−\mathrm{i}\theta} }{\mathrm{2}}\right)^{\mathrm{2}} \:+\left(\frac{\mathrm{e}^{\mathrm{i}\theta} −\mathrm{e}^{−\mathrm{i}\theta} }{\mathrm{2i}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\:\mathrm{e}^{\mathrm{2i}\theta} \:+\mathrm{2}\:+\mathrm{e}^{−\mathrm{2i}\theta} \right)−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{e}^{\mathrm{2i}\theta} −\mathrm{2}\:+\mathrm{e}^{−\mathrm{2i}\theta} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\mathrm{e}^{\mathrm{2i}\theta\:} \:+\mathrm{2}+\mathrm{e}^{−\mathrm{2i}\theta} −\mathrm{e}^{\mathrm{2i}\theta} +\mathrm{2}−\mathrm{e}^{−\mathrm{2i}\theta} \right\}\:=\frac{\mathrm{4}}{\mathrm{4}}\:=\mathrm{1} \\ $$
Commented by mohammad17 last updated on 15/Sep/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 16/Sep/20
you are welcome
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by mathmax by abdo last updated on 15/Sep/20
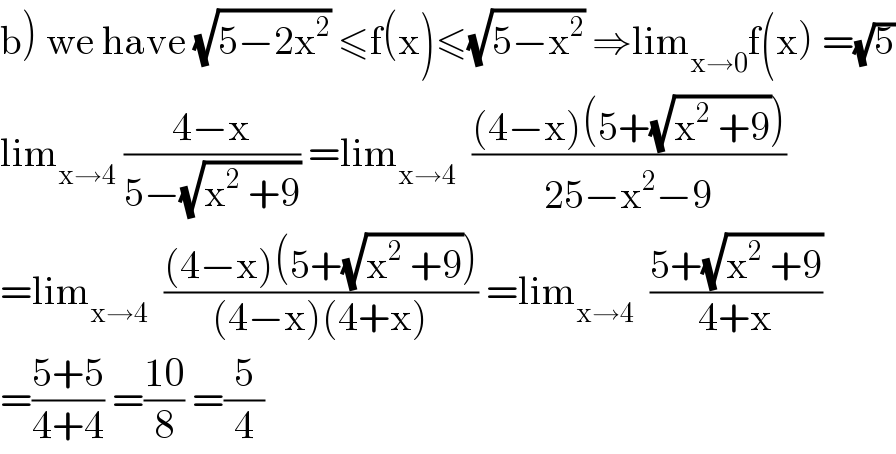
b) we have (√(5−2x^2 )) ≤f(x)≤(√(5−x^2 )) ⇒lim_(x→0) f(x) =(√5) lim_(x→4) ((4−x)/(5−(√(x^2 +9)))) =lim_(x→4) (((4−x)(5+(√(x^2 +9))))/(25−x^2 −9)) =lim_(x→4) (((4−x)(5+(√(x^2 +9))))/((4−x)(4+x))) =lim_(x→4) ((5+(√(x^2 +9)))/(4+x)) =((5+5)/(4+4)) =((10)/8) =(5/4)
$$\left.\mathrm{b}\right)\:\mathrm{we}\:\mathrm{have}\:\sqrt{\mathrm{5}−\mathrm{2x}^{\mathrm{2}} }\:\leqslant\mathrm{f}\left(\mathrm{x}\right)\leqslant\sqrt{\mathrm{5}−\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\sqrt{\mathrm{5}} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{4}} \:\frac{\mathrm{4}−\mathrm{x}}{\mathrm{5}−\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{4}} \:\:\frac{\left(\mathrm{4}−\mathrm{x}\right)\left(\mathrm{5}+\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\right)}{\mathrm{25}−\mathrm{x}^{\mathrm{2}} −\mathrm{9}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{4}} \:\:\frac{\left(\mathrm{4}−\mathrm{x}\right)\left(\mathrm{5}+\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\right)}{\left(\mathrm{4}−\mathrm{x}\right)\left(\mathrm{4}+\mathrm{x}\right)}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{4}} \:\:\frac{\mathrm{5}+\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}}{\mathrm{4}+\mathrm{x}} \\ $$$$=\frac{\mathrm{5}+\mathrm{5}}{\mathrm{4}+\mathrm{4}}\:=\frac{\mathrm{10}}{\mathrm{8}}\:=\frac{\mathrm{5}}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 15/Sep/20
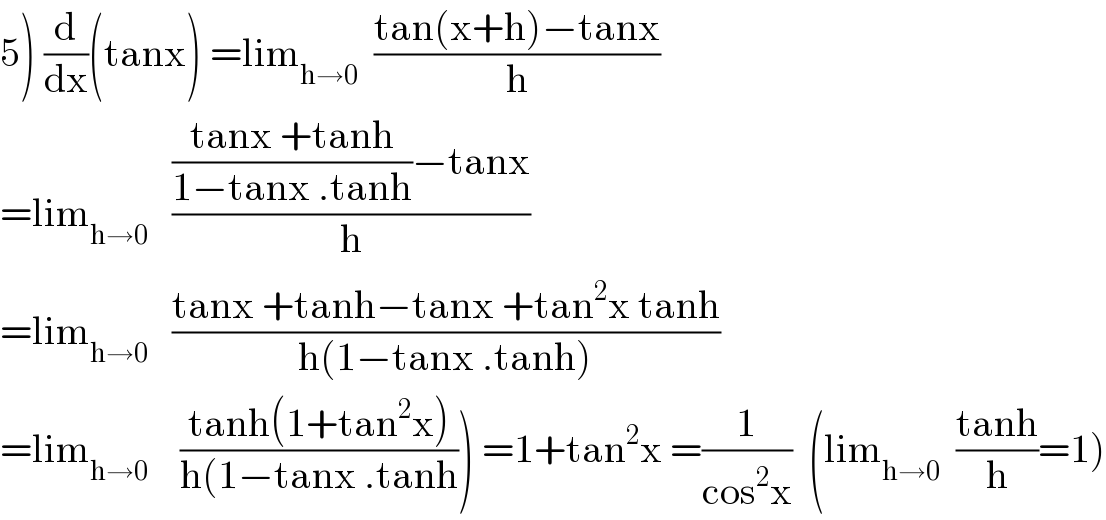
5) (d/dx)(tanx) =lim_(h→0) ((tan(x+h)−tanx)/h) =lim_(h→0) ((((tanx +tanh)/(1−tanx .tanh))−tanx)/h) =lim_(h→0) ((tanx +tanh−tanx +tan^2 x tanh)/(h(1−tanx .tanh))) =lim_(h→0) ((tanh(1+tan^2 x))/(h(1−tanx .tanh))) =1+tan^2 x =(1/(cos^2 x)) (lim_(h→0) ((tanh)/h)=1)
$$\left.\mathrm{5}\right)\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{tanx}\right)\:=\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{tan}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{tanx}}{\mathrm{h}} \\ $$$$=\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\:\:\frac{\frac{\mathrm{tanx}\:+\mathrm{tanh}}{\mathrm{1}−\mathrm{tanx}\:.\mathrm{tanh}}−\mathrm{tanx}}{\mathrm{h}} \\ $$$$=\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{tanx}\:+\mathrm{tanh}−\mathrm{tanx}\:+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{tanh}}{\mathrm{h}\left(\mathrm{1}−\mathrm{tanx}\:.\mathrm{tanh}\right)} \\ $$$$\left.=\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\:\:\:\frac{\mathrm{tanh}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{h}\left(\mathrm{1}−\mathrm{tanx}\:.\mathrm{tanh}\right.}\right)\:=\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\:\left(\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{tanh}}{\mathrm{h}}=\mathrm{1}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *