Question Number 113781 by Ar Brandon last updated on 15/Sep/20

Answered by Dwaipayan Shikari last updated on 15/Sep/20
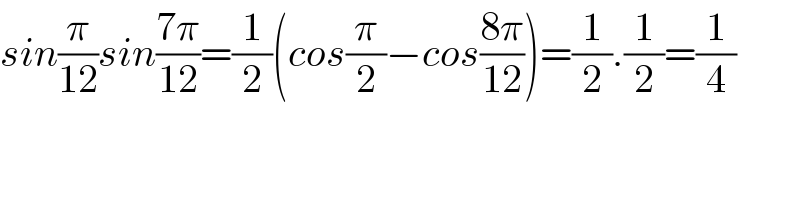
$${sin}\frac{\pi}{\mathrm{12}}{sin}\frac{\mathrm{7}\pi}{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\frac{\pi}{\mathrm{2}}−{cos}\frac{\mathrm{8}\pi}{\mathrm{12}}\right)=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by Dwaipayan Shikari last updated on 15/Sep/20
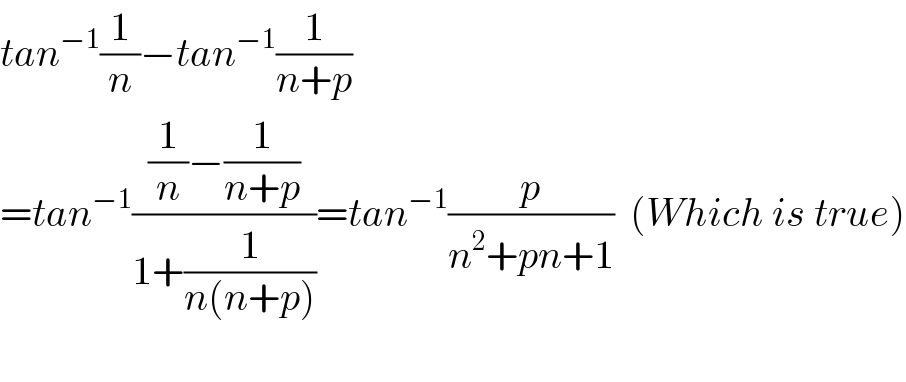
$${tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{n}}−{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{n}+{p}} \\ $$$$={tan}^{−\mathrm{1}} \frac{\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+{p}}}{\mathrm{1}+\frac{\mathrm{1}}{{n}\left({n}+{p}\right)}}={tan}^{−\mathrm{1}} \frac{{p}}{{n}^{\mathrm{2}} +{pn}+\mathrm{1}}\:\:\left({Which}\:{is}\:{true}\right) \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 15/Sep/20
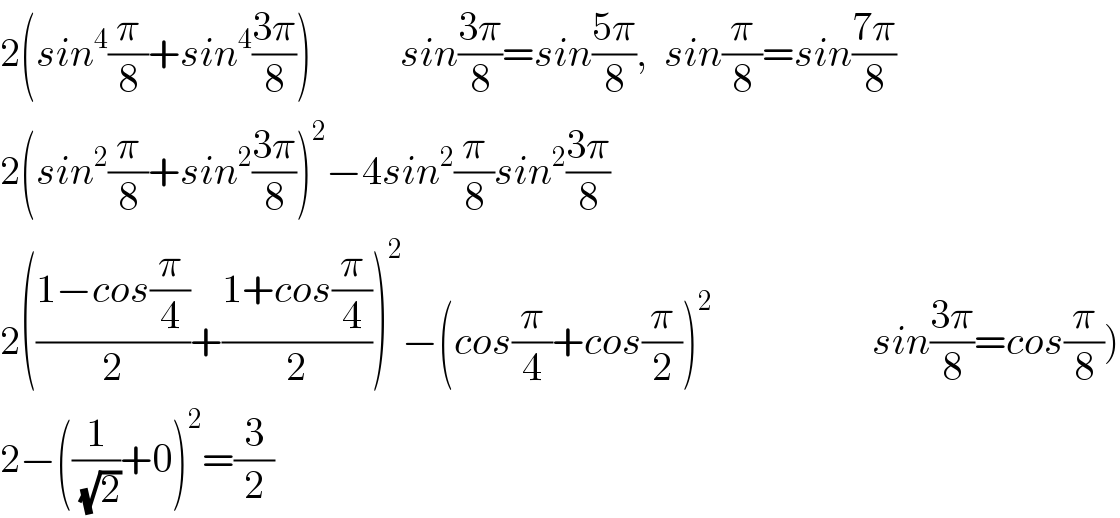
$$\mathrm{2}\left({sin}^{\mathrm{4}} \frac{\pi}{\mathrm{8}}+{sin}^{\mathrm{4}} \frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:\:\:\:\:\:\:\:\:\:\:{sin}\frac{\mathrm{3}\pi}{\mathrm{8}}={sin}\frac{\mathrm{5}\pi}{\mathrm{8}},\:\:{sin}\frac{\pi}{\mathrm{8}}={sin}\frac{\mathrm{7}\pi}{\mathrm{8}} \\ $$$$\mathrm{2}\left({sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}+{sin}^{\mathrm{2}} \frac{\mathrm{3}\pi}{\mathrm{8}}\right)^{\mathrm{2}} −\mathrm{4}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}{sin}^{\mathrm{2}} \frac{\mathrm{3}\pi}{\mathrm{8}} \\ $$$$\left.\mathrm{2}\left(\frac{\mathrm{1}−{cos}\frac{\pi}{\mathrm{4}}}{\mathrm{2}}+\frac{\mathrm{1}+{cos}\frac{\pi}{\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({cos}\frac{\pi}{\mathrm{4}}+{cos}\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{sin}\frac{\mathrm{3}\pi}{\mathrm{8}}={cos}\frac{\pi}{\mathrm{8}}\right) \\ $$$$\mathrm{2}−\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\mathrm{0}\right)^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 15/Sep/20
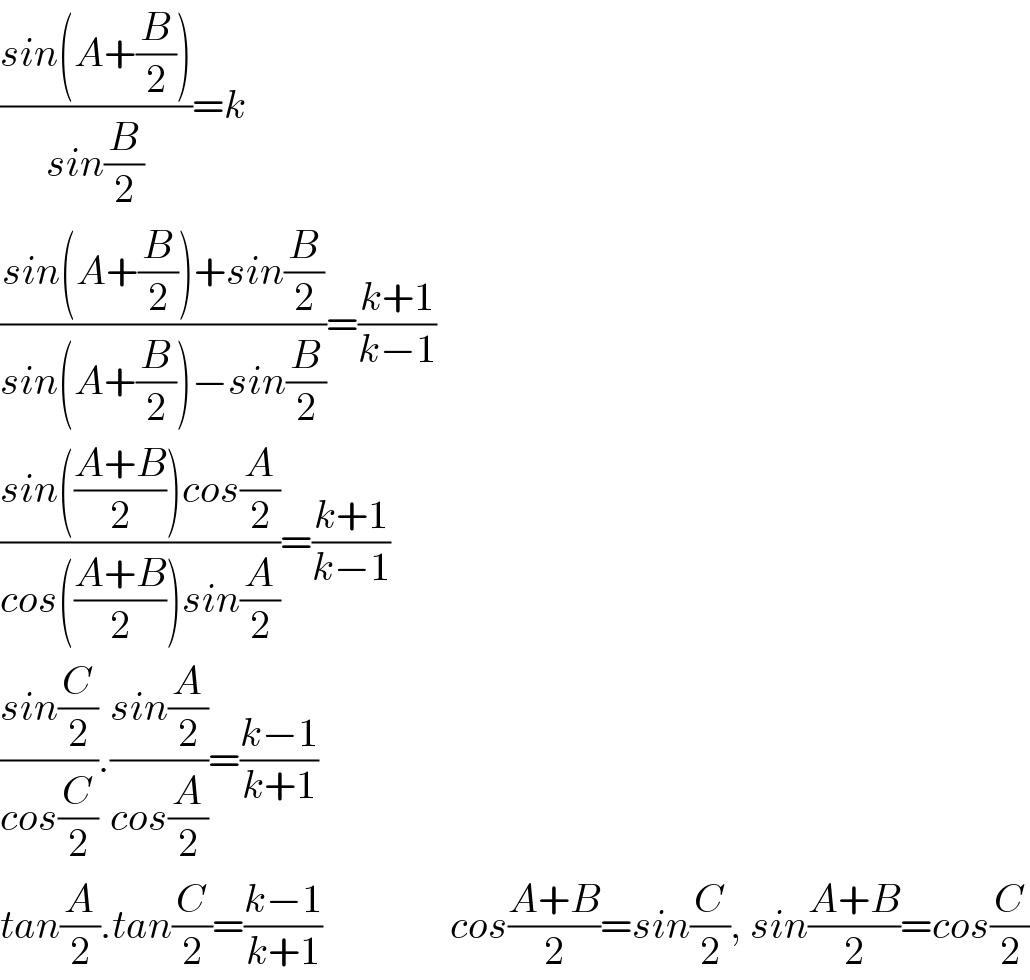
$$\frac{{sin}\left({A}+\frac{{B}}{\mathrm{2}}\right)}{{sin}\frac{{B}}{\mathrm{2}}}={k} \\ $$$$\frac{{sin}\left({A}+\frac{{B}}{\mathrm{2}}\right)+{sin}\frac{{B}}{\mathrm{2}}}{{sin}\left({A}+\frac{{B}}{\mathrm{2}}\right)−{sin}\frac{{B}}{\mathrm{2}}}=\frac{{k}+\mathrm{1}}{{k}−\mathrm{1}} \\ $$$$\frac{{sin}\left(\frac{{A}+{B}}{\mathrm{2}}\right){cos}\frac{{A}}{\mathrm{2}}}{{cos}\left(\frac{{A}+{B}}{\mathrm{2}}\right){sin}\frac{{A}}{\mathrm{2}}}=\frac{{k}+\mathrm{1}}{{k}−\mathrm{1}} \\ $$$$\frac{{sin}\frac{{C}}{\mathrm{2}}}{{cos}\frac{{C}}{\mathrm{2}}}.\frac{{sin}\frac{{A}}{\mathrm{2}}}{{cos}\frac{{A}}{\mathrm{2}}}=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}} \\ $$$${tan}\frac{{A}}{\mathrm{2}}.{tan}\frac{{C}}{\mathrm{2}}=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{cos}\frac{{A}+{B}}{\mathrm{2}}={sin}\frac{{C}}{\mathrm{2}},\:{sin}\frac{{A}+{B}}{\mathrm{2}}={cos}\frac{{C}}{\mathrm{2}} \\ $$
