Menu Close

Question-113894

Tinku Tara 0 Comments
Pin




Question Number 113894 by Aina Samuel Temidayo last updated on 16/Sep/20
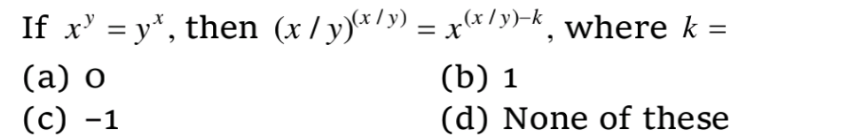
Commented by MJS_new last updated on 16/Sep/20
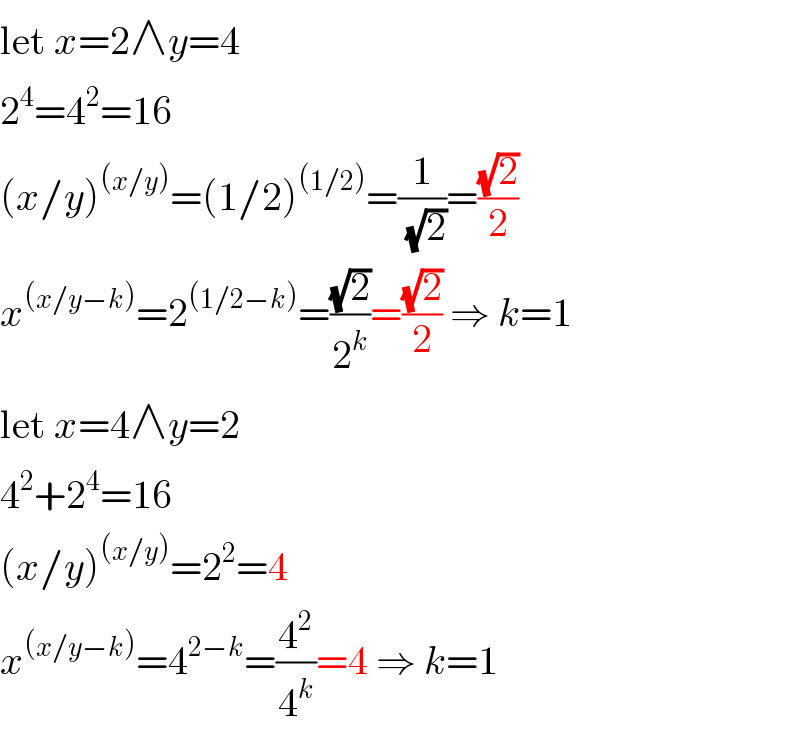
let x=2∧y=4 2^4 =4^2 =16 (x/y)^((x/y)) =(1/2)^((1/2)) =(1/( (√2)))=((√2)/2) x^((x/y−k)) =2^((1/2−k)) =((√2)/2^k )=((√2)/2) ⇒ k=1 let x=4∧y=2 4^2 +2^4 =16 (x/y)^((x/y)) =2^2 =4 x^((x/y−k)) =4^(2−k) =(4^2 /4^k )=4 ⇒ k=1
$$\mathrm{let}\:{x}=\mathrm{2}\wedge{y}=\mathrm{4} \\ $$$$\mathrm{2}^{\mathrm{4}} =\mathrm{4}^{\mathrm{2}} =\mathrm{16} \\ $$$$\left({x}/{y}\right)^{\left({x}/{y}\right)} =\left(\mathrm{1}/\mathrm{2}\right)^{\left(\mathrm{1}/\mathrm{2}\right)} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${x}^{\left({x}/{y}−{k}\right)} =\mathrm{2}^{\left(\mathrm{1}/\mathrm{2}−{k}\right)} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}^{{k}} }=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\Rightarrow\:{k}=\mathrm{1} \\ $$$$\mathrm{let}\:{x}=\mathrm{4}\wedge{y}=\mathrm{2} \\ $$$$\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{4}} =\mathrm{16} \\ $$$$\left({x}/{y}\right)^{\left({x}/{y}\right)} =\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$${x}^{\left({x}/{y}−{k}\right)} =\mathrm{4}^{\mathrm{2}−{k}} =\frac{\mathrm{4}^{\mathrm{2}} }{\mathrm{4}^{{k}} }=\mathrm{4}\:\Rightarrow\:{k}=\mathrm{1} \\ $$
Answered by MJS_new last updated on 16/Sep/20
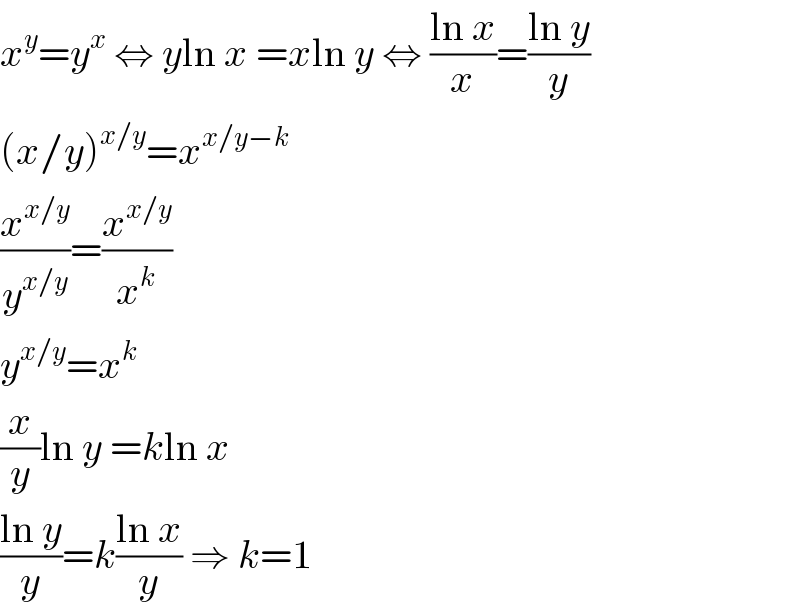
x^y =y^x ⇔ yln x =xln y ⇔ ((ln x)/x)=((ln y)/y) (x/y)^(x/y) =x^(x/y−k) (x^(x/y) /y^(x/y) )=(x^(x/y) /x^k ) y^(x/y) =x^k (x/y)ln y =kln x ((ln y)/y)=k((ln x)/y) ⇒ k=1
$${x}^{{y}} ={y}^{{x}} \:\Leftrightarrow\:{y}\mathrm{ln}\:{x}\:={x}\mathrm{ln}\:{y}\:\Leftrightarrow\:\frac{\mathrm{ln}\:{x}}{{x}}=\frac{\mathrm{ln}\:{y}}{{y}} \\ $$$$\left({x}/{y}\right)^{{x}/{y}} ={x}^{{x}/{y}−{k}} \\ $$$$\frac{{x}^{{x}/{y}} }{{y}^{{x}/{y}} }=\frac{{x}^{{x}/{y}} }{{x}^{{k}} } \\ $$$${y}^{{x}/{y}} ={x}^{{k}} \\ $$$$\frac{{x}}{{y}}\mathrm{ln}\:{y}\:={k}\mathrm{ln}\:{x} \\ $$$$\frac{\mathrm{ln}\:{y}}{{y}}={k}\frac{\mathrm{ln}\:{x}}{{y}}\:\Rightarrow\:{k}=\mathrm{1} \\ $$
Commented by Aina Samuel Temidayo last updated on 16/Sep/20
Sorry, I don′t understand your last two steps.
$$\mathrm{Sorry},\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{your}\:\mathrm{last} \\ $$$$\mathrm{two}\:\mathrm{steps}. \\ $$
Commented by MJS_new last updated on 16/Sep/20
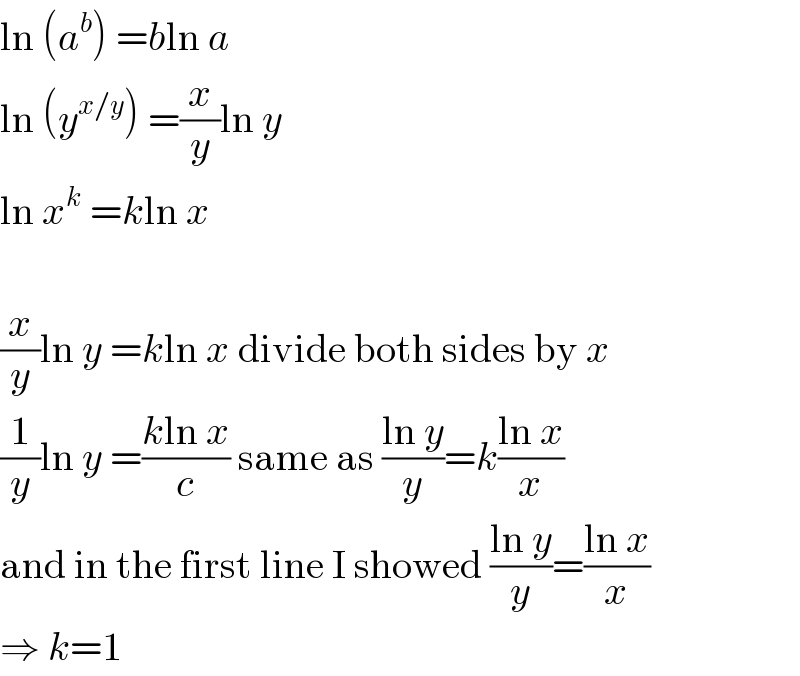
ln (a^b ) =bln a ln (y^(x/y) ) =(x/y)ln y ln x^k =kln x (x/y)ln y =kln x divide both sides by x (1/y)ln y =((kln x)/c) same as ((ln y)/y)=k((ln x)/x) and in the first line I showed ((ln y)/y)=((ln x)/x) ⇒ k=1
$$\mathrm{ln}\:\left({a}^{{b}} \right)\:={b}\mathrm{ln}\:{a} \\ $$$$\mathrm{ln}\:\left({y}^{{x}/{y}} \right)\:=\frac{{x}}{{y}}\mathrm{ln}\:{y} \\ $$$$\mathrm{ln}\:{x}^{{k}} \:={k}\mathrm{ln}\:{x} \\ $$$$ \\ $$$$\frac{{x}}{{y}}\mathrm{ln}\:{y}\:={k}\mathrm{ln}\:{x}\:\mathrm{divide}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{by}\:{x} \\ $$$$\frac{\mathrm{1}}{{y}}\mathrm{ln}\:{y}\:=\frac{{k}\mathrm{ln}\:{x}}{{c}}\:\mathrm{same}\:\mathrm{as}\:\frac{\mathrm{ln}\:{y}}{{y}}={k}\frac{\mathrm{ln}\:{x}}{{x}} \\ $$$$\mathrm{and}\:\mathrm{in}\:\mathrm{the}\:\mathrm{first}\:\mathrm{line}\:\mathrm{I}\:\mathrm{showed}\:\frac{\mathrm{ln}\:{y}}{{y}}=\frac{\mathrm{ln}\:{x}}{{x}} \\ $$$$\Rightarrow\:{k}=\mathrm{1} \\ $$
Answered by john santu last updated on 16/Sep/20
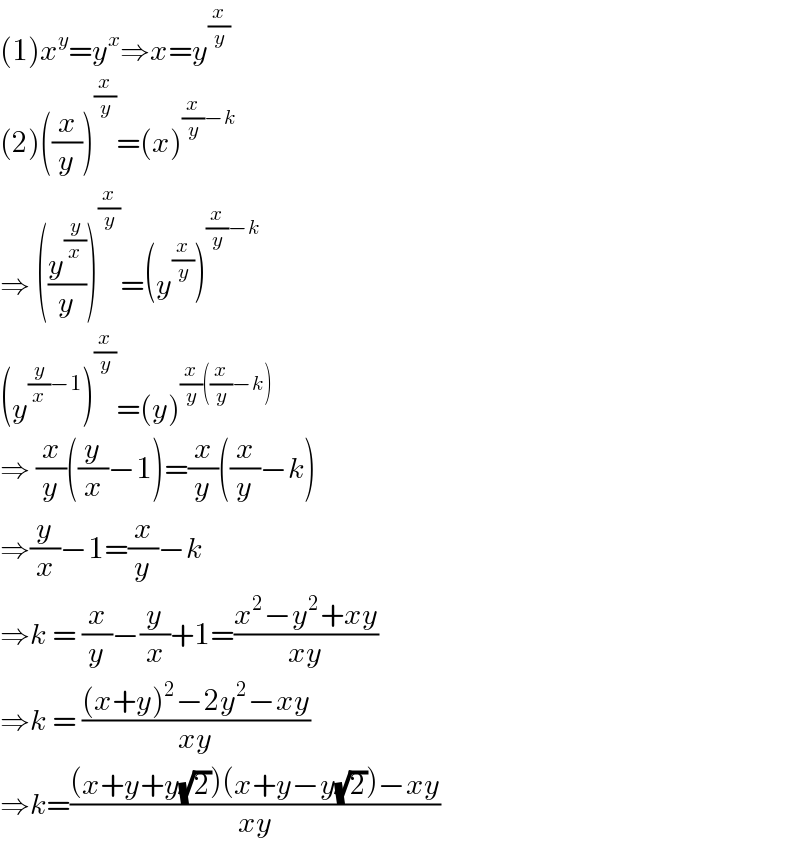
(1)x^y =y^x ⇒x=y^(x/y) (2)((x/y))^(x/y) =(x)^((x/y)−k) ⇒ ((y^(y/x) /y))^(x/y) =(y^(x/y) )^((x/y)−k) (y^((y/x)−1) )^(x/y) =(y)^((x/y)((x/y)−k)) ⇒ (x/y)((y/x)−1)=(x/y)((x/y)−k) ⇒(y/x)−1=(x/y)−k ⇒k = (x/y)−(y/x)+1=((x^2 −y^2 +xy)/(xy)) ⇒k = (((x+y)^2 −2y^2 −xy)/(xy)) ⇒k=(((x+y+y(√2))(x+y−y(√2))−xy)/(xy))
$$\left(\mathrm{1}\right){x}^{{y}} ={y}^{{x}} \Rightarrow{x}={y}^{\frac{{x}}{{y}}} \\ $$$$\left(\mathrm{2}\right)\left(\frac{{x}}{{y}}\right)^{\frac{{x}}{{y}}} =\left({x}\right)^{\frac{{x}}{{y}}−{k}} \\ $$$$\Rightarrow\:\left(\frac{{y}^{\frac{{y}}{{x}}} }{{y}}\right)^{\frac{{x}}{{y}}} =\left({y}^{\frac{{x}}{{y}}} \right)^{\frac{{x}}{{y}}−{k}} \\ $$$$\left({y}^{\frac{{y}}{{x}}−\mathrm{1}} \right)^{\frac{{x}}{{y}}} =\left({y}\right)^{\frac{{x}}{{y}}\left(\frac{{x}}{{y}}−{k}\right)} \\ $$$$\Rightarrow\:\frac{{x}}{{y}}\left(\frac{{y}}{{x}}−\mathrm{1}\right)=\frac{{x}}{{y}}\left(\frac{{x}}{{y}}−{k}\right) \\ $$$$\Rightarrow\frac{{y}}{{x}}−\mathrm{1}=\frac{{x}}{{y}}−{k}\: \\ $$$$\Rightarrow{k}\:=\:\frac{{x}}{{y}}−\frac{{y}}{{x}}+\mathrm{1}=\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{xy}}{{xy}} \\ $$$$\Rightarrow{k}\:=\:\frac{\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{y}^{\mathrm{2}} −{xy}}{{xy}} \\ $$$$\Rightarrow{k}=\frac{\left({x}+{y}+{y}\sqrt{\mathrm{2}}\right)\left({x}+{y}−{y}\sqrt{\mathrm{2}}\right)−{xy}}{{xy}} \\ $$
Commented by MJS_new last updated on 16/Sep/20
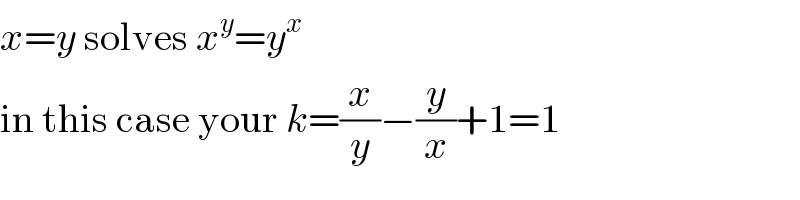
x=y solves x^y =y^x in this case your k=(x/y)−(y/x)+1=1
$${x}={y}\:\mathrm{solves}\:{x}^{{y}} ={y}^{{x}} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{your}\:{k}=\frac{{x}}{{y}}−\frac{{y}}{{x}}+\mathrm{1}=\mathrm{1} \\ $$
Commented by MJS_new last updated on 16/Sep/20
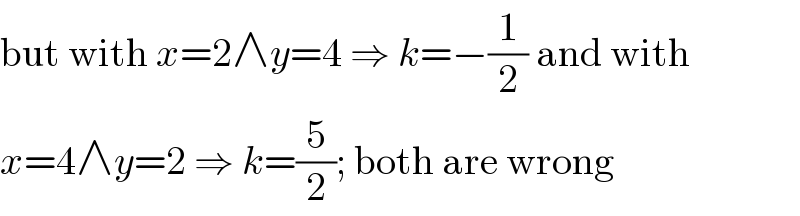
but with x=2∧y=4 ⇒ k=−(1/2) and with x=4∧y=2 ⇒ k=(5/2); both are wrong
$$\mathrm{but}\:\mathrm{with}\:{x}=\mathrm{2}\wedge{y}=\mathrm{4}\:\Rightarrow\:{k}=−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{with} \\ $$$${x}=\mathrm{4}\wedge{y}=\mathrm{2}\:\Rightarrow\:{k}=\frac{\mathrm{5}}{\mathrm{2}};\:\mathrm{both}\:\mathrm{are}\:\mathrm{wrong} \\ $$
Commented by bobhans last updated on 16/Sep/20
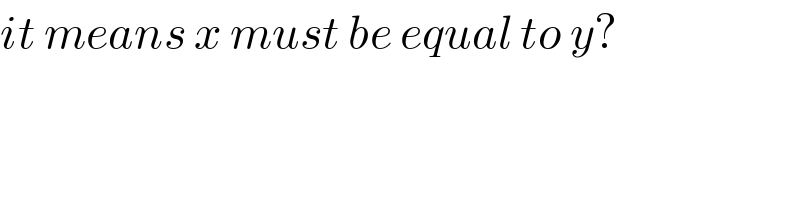
it means x must be equal to y?
$${it}\:{means}\:{x}\:{must}\:{be}\:{equal}\:{to}\:{y}? \\ $$
Commented by MJS_new last updated on 16/Sep/20
no, see my answer above
$$\mathrm{no},\:\mathrm{see}\:\mathrm{my}\:{answer}\:\mathrm{above} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *