Question-113996

Question Number 113996 by Aina Samuel Temidayo last updated on 16/Sep/20

Commented by MJS_new last updated on 16/Sep/20

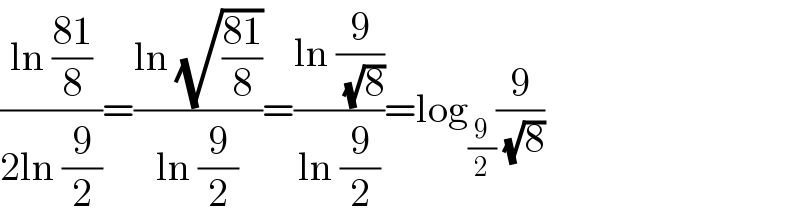
((ln ((81)/8))/(2ln (9/2)))=((ln (√((81)/8)))/(ln (9/2)))=((ln (9/( (√8))))/(ln (9/2)))=log_(9/2) (9/( (√8)))

$$\frac{\mathrm{ln}\:\frac{\mathrm{81}}{\mathrm{8}}}{\mathrm{2ln}\:\frac{\mathrm{9}}{\mathrm{2}}}=\frac{\mathrm{ln}\:\sqrt{\frac{\mathrm{81}}{\mathrm{8}}}}{\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{2}}}=\frac{\mathrm{ln}\:\frac{\mathrm{9}}{\:\sqrt{\mathrm{8}}}}{\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{2}}}=\mathrm{log}_{\frac{\mathrm{9}}{\mathrm{2}}} \frac{\mathrm{9}}{\:\sqrt{\mathrm{8}}} \\ $$

Answered by bobhans last updated on 17/Sep/20

9^x +(1/3).9^x = 2(√2) .2^x +(√2).2^x ⇒(4/3).9^x = 3(√2).2^x ⇒9^(x−1) = 2^(x−(3/2)) ; (x−1)ln (9)=(x−(3/2))ln (2) xln 9−xln 2 = ln 9−(3/2)ln 2 x.ln ((9/2)) = ln ((9/(2(√2)))) ⇒ x= log _(9/2) ((9/( (√8))))

$$\mathrm{9}^{{x}} +\frac{\mathrm{1}}{\mathrm{3}}.\mathrm{9}^{{x}} \:=\:\mathrm{2}\sqrt{\mathrm{2}}\:.\mathrm{2}^{{x}} +\sqrt{\mathrm{2}}.\mathrm{2}^{{x}} \\ $$$$\Rightarrow\frac{\mathrm{4}}{\mathrm{3}}.\mathrm{9}^{{x}} \:=\:\mathrm{3}\sqrt{\mathrm{2}}.\mathrm{2}^{{x}} \\ $$$$\Rightarrow\mathrm{9}^{{x}−\mathrm{1}} \:=\:\mathrm{2}^{{x}−\frac{\mathrm{3}}{\mathrm{2}}} \:;\:\left({x}−\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{9}\right)=\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$$${x}\mathrm{ln}\:\mathrm{9}−{x}\mathrm{ln}\:\mathrm{2}\:=\:\mathrm{ln}\:\mathrm{9}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2} \\ $$$${x}.\mathrm{ln}\:\left(\frac{\mathrm{9}}{\mathrm{2}}\right)\:=\:\mathrm{ln}\:\left(\frac{\mathrm{9}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\:\Rightarrow\:{x}=\:\mathrm{log}\:_{\frac{\mathrm{9}}{\mathrm{2}}} \left(\frac{\mathrm{9}}{\:\sqrt{\mathrm{8}}}\right) \\ $$

Facebook Tweet Pin

Question-113996

Leave a Reply Cancel reply