Menu Close

Question-113997

Tinku Tara 0 Comments
Pin




Question Number 113997 by Aina Samuel Temidayo last updated on 16/Sep/20
Answered by bobhans last updated on 16/Sep/20
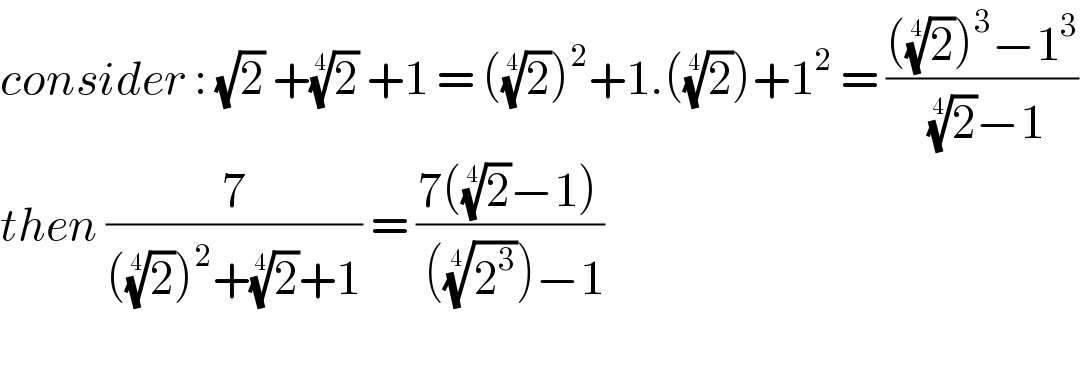
consider : (√2) +(2)^(1/4) +1 = ((2)^(1/4) )^2 +1.((2)^(1/4) )+1^2 = ((((2)^(1/4) )^3 −1^3 )/( (2)^(1/4) −1)) then (7/(((2)^(1/4) )^2 +(2)^(1/4) +1)) = ((7((2)^(1/4) −1))/( ((2^3 )^(1/4) )−1))
$${consider}\::\:\sqrt{\mathrm{2}}\:+\sqrt[{\mathrm{4}}]{\mathrm{2}}\:+\mathrm{1}\:=\:\left(\sqrt[{\mathrm{4}}]{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}.\left(\sqrt[{\mathrm{4}}]{\mathrm{2}}\right)+\mathrm{1}^{\mathrm{2}} \:=\:\frac{\left(\sqrt[{\mathrm{4}}]{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{1}^{\mathrm{3}} }{\:\sqrt[{\mathrm{4}}]{\mathrm{2}}−\mathrm{1}} \\ $$$${then}\:\frac{\mathrm{7}}{\left(\sqrt[{\mathrm{4}}]{\mathrm{2}}\right)^{\mathrm{2}} +\sqrt[{\mathrm{4}}]{\mathrm{2}}+\mathrm{1}}\:=\:\frac{\mathrm{7}\left(\sqrt[{\mathrm{4}}]{\mathrm{2}}−\mathrm{1}\right)}{\:\left(\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{3}} }\right)−\mathrm{1}} \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 16/Sep/20
(7/(2^(1/2) +2^(1/4) +1))=A+B.2^(1/4) +C.2^(1/2) +D.2^(3/4) ⇔(2^(1/2) +2^(1/4) +1)(A+B.2^(1/4) +C.2^(1/2) +D.2^(3/4) )=7 ⇔A.2^(1/2) +A.2^(1/4) +A+B.2^(3/4) +B.2^(1/2) +B.2^(1/4) +2C+C.2^(3/4) +C.2^(1/2) +D.2^(5/4) +D.2+D.2^(3/3) =(A+2C+2D)+(A+B+C).2^(1/2) +(A+B+2D).2^(1/4) +(B+C+D)^(3/4) =7 ⇔ { ((A+2C+2D=7(sinceD. 2^(5/4) =2D.2^(1/4) ))),((A+B+C=0)),((A+B+2D=0)),((B+C+D=0)) :} Solve above system we get: A=1,B=−3,C=2,D=1 Hence,there are three true options in available answer
$$\frac{\mathrm{7}}{\mathrm{2}^{\mathrm{1}/\mathrm{2}} +\mathrm{2}^{\mathrm{1}/\mathrm{4}} +\mathrm{1}}=\mathrm{A}+\mathrm{B}.\mathrm{2}^{\mathrm{1}/\mathrm{4}} +\mathrm{C}.\mathrm{2}^{\mathrm{1}/\mathrm{2}} +\mathrm{D}.\mathrm{2}^{\mathrm{3}/\mathrm{4}} \\ $$$$\Leftrightarrow\left(\mathrm{2}^{\mathrm{1}/\mathrm{2}} +\mathrm{2}^{\mathrm{1}/\mathrm{4}} +\mathrm{1}\right)\left(\mathrm{A}+\mathrm{B}.\mathrm{2}^{\mathrm{1}/\mathrm{4}} +\mathrm{C}.\mathrm{2}^{\mathrm{1}/\mathrm{2}} +\mathrm{D}.\mathrm{2}^{\mathrm{3}/\mathrm{4}} \right)=\mathrm{7} \\ $$$$\Leftrightarrow\mathrm{A}.\mathrm{2}^{\mathrm{1}/\mathrm{2}} +\mathrm{A}.\mathrm{2}^{\mathrm{1}/\mathrm{4}} +\mathrm{A}+\mathrm{B}.\mathrm{2}^{\mathrm{3}/\mathrm{4}} +\mathrm{B}.\mathrm{2}^{\mathrm{1}/\mathrm{2}} +\mathrm{B}.\mathrm{2}^{\mathrm{1}/\mathrm{4}} \\ $$$$+\mathrm{2C}+\mathrm{C}.\mathrm{2}^{\mathrm{3}/\mathrm{4}} +\mathrm{C}.\mathrm{2}^{\mathrm{1}/\mathrm{2}} +\mathrm{D}.\mathrm{2}^{\mathrm{5}/\mathrm{4}} +\mathrm{D}.\mathrm{2}+\mathrm{D}.\mathrm{2}^{\mathrm{3}/\mathrm{3}} \\ $$$$=\left(\mathrm{A}+\mathrm{2C}+\mathrm{2D}\right)+\left(\mathrm{A}+\mathrm{B}+\mathrm{C}\right).\mathrm{2}^{\mathrm{1}/\mathrm{2}} \\ $$$$+\left(\mathrm{A}+\mathrm{B}+\mathrm{2D}\right).\mathrm{2}^{\mathrm{1}/\mathrm{4}} +\left(\mathrm{B}+\mathrm{C}+\mathrm{D}\right)^{\mathrm{3}/\mathrm{4}} =\mathrm{7} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{A}+\mathrm{2C}+\mathrm{2D}=\mathrm{7}\left(\mathrm{sinceD}.\:\mathrm{2}^{\mathrm{5}/\mathrm{4}} =\mathrm{2D}.\mathrm{2}^{\mathrm{1}/\mathrm{4}} \right)}\\{\mathrm{A}+\mathrm{B}+\mathrm{C}=\mathrm{0}}\\{\mathrm{A}+\mathrm{B}+\mathrm{2D}=\mathrm{0}}\\{\mathrm{B}+\mathrm{C}+\mathrm{D}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{Solve}\:\mathrm{above}\:\mathrm{system}\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{A}=\mathrm{1},\mathrm{B}=−\mathrm{3},\mathrm{C}=\mathrm{2},\mathrm{D}=\mathrm{1} \\ $$$$\mathrm{Hence},\mathrm{there}\:\mathrm{are}\:\mathrm{three}\:\mathrm{true}\:\mathrm{options} \\ $$$$\mathrm{in}\:\mathrm{available}\:\mathrm{answer} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *