Question Number 114290 by mathdave last updated on 18/Sep/20

Answered by 1549442205PVT last updated on 18/Sep/20

$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\overline {\mathrm{abc}},\overline {\mathrm{bca}},\overline {\mathrm{cab}} \\ $$$$\mathrm{form}\:\mathrm{a}\:\mathrm{G}.\mathrm{P}\:\mathrm{we}\:\mathrm{infer}\:\overline {\mathrm{abc}}×\overline {\mathrm{cab}}=\left(\overline {\mathrm{bca}}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\left(\left(\mathrm{100a}+\mathrm{10b}+\mathrm{c}\right)\left(\mathrm{100c}+\mathrm{10a}+\mathrm{b}\right)=\right. \\ $$$$\left(\mathrm{100b}+\mathrm{10c}+\mathrm{a}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{10000ac}+\mathrm{1000bc}+\mathrm{100c}^{\mathrm{2}} +\mathrm{1000a}^{\mathrm{2}} \\ $$$$+\mathrm{100ab}+\mathrm{10ac}+\mathrm{100ab}+\mathrm{10b}^{\mathrm{2}} +\mathrm{bc} \\ $$$$=\mathrm{10000b}^{\mathrm{2}} +\mathrm{100c}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} +\mathrm{2000bc}+\mathrm{200ab}+\mathrm{20ac} \\ $$$$\Leftrightarrow\mathrm{9990ac}−\mathrm{999bc}−\mathrm{9990b}^{\mathrm{2}} +\mathrm{999a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{10ac}=\mathrm{10b}^{\mathrm{2}} +\mathrm{bc} \\ $$$$\Leftrightarrow\left(\mathrm{a}+\mathrm{5c}\right)^{\mathrm{2}} =\mathrm{25c}^{\mathrm{2}} +\mathrm{10b}^{\mathrm{2}} +\mathrm{bc} \\ $$$$\Leftrightarrow\mathrm{100}\left(\mathrm{a}+\mathrm{5c}\right)^{\mathrm{2}} =\mathrm{2500c}^{\mathrm{2}} +\mathrm{100bc}+\mathrm{1000b}^{\mathrm{2}} \\ $$$$\Leftrightarrow\left(\mathrm{10a}+\mathrm{50c}\right)^{\mathrm{2}} =\left(\mathrm{50c}+\mathrm{b}\right)^{\mathrm{2}} +\mathrm{999b}^{\mathrm{2}} \\ $$$$\Leftrightarrow\left(\mathrm{10a}+\mathrm{100c}+\mathrm{b}\right)\left(\mathrm{10a}−\mathrm{b}\right)=\mathrm{999b}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$=\mathrm{37}.\mathrm{27}.\mathrm{b}^{\mathrm{2}} \Rightarrow\mathrm{LHS}\vdots\mathrm{37} \\ $$$$\left.\mathrm{i}\right)\mathrm{If}\:\mathrm{b}=\mathrm{9}\:\mathrm{then}\:\mathrm{it}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\: \\ $$$$\mathrm{10a}−\mathrm{b}\:\mathrm{isn}'\mathrm{t}\:\mathrm{divisible}\:\mathrm{37}.\mathrm{Hence} \\ $$$$\mathrm{10a}+\mathrm{100c}+\mathrm{9}\vdots\mathrm{37}.\mathrm{Since}\:\mathrm{10a}+\mathrm{100c}+\mathrm{9}>\mathrm{111} \\ $$$$\mathrm{and}\left(\mathrm{10a}+\mathrm{100c}+\mathrm{9}\right)=\mathrm{37k}\Rightarrow\mathrm{37k}−\mathrm{9}\vdots\mathrm{10} \\ $$$$\Rightarrow\mathrm{37k}=\mathrm{999}\Rightarrow\mathrm{10a}−\mathrm{9}=\mathrm{81}\Rightarrow\mathrm{a}=\mathrm{9} \\ $$$$\left.+\right)\mathrm{If}\:\mathrm{10}.\mathrm{9}+\mathrm{100c}+\mathrm{9}=\mathrm{999}\Rightarrow\mathrm{c}=\mathrm{9} \\ $$$$\mathrm{We}\:\mathrm{get}\:\overline {\mathrm{abc}}=\mathrm{999} \\ $$$$\left.\mathrm{ii}\right)\mathrm{If}\:\mathrm{b}=\mathrm{8}\:\mathrm{then}\:\mathrm{10a}−\mathrm{8}\:\mathrm{isn}'\mathrm{t}\:\mathrm{divisible}\:\mathrm{37} \\ $$$$\mathrm{10a}+\mathrm{100c}+\mathrm{8}=\mathrm{37k}\Rightarrow\mathrm{37k}−\mathrm{8}\vdots\mathrm{10} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{impossible}\:\mathrm{since}\:\mathrm{37k}\in\left\{\mathrm{259},\mathrm{629},\mathrm{999}\right\} \\ $$$$\mathrm{By}\:\mathrm{similar}\:\mathrm{argument}\:\mathrm{for}\:\mathrm{the}\:\mathrm{cases} \\ $$$$\mathrm{b}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{7}\:\mathrm{we}\:\mathrm{see}\:\mathrm{that}\:\nexists\mathrm{a},\mathrm{c} \\ $$$$\mathrm{satisfying}\left(\mathrm{2}\right) \\ $$$$\mathrm{Thus},\mathrm{there}\:\mathrm{is}\:\mathrm{only}\:\mathrm{one}\:\mathrm{three}−\mathrm{digits}\:\: \\ $$$$\mathrm{number}\:\overline {\mathrm{abc}}=\mathrm{999}\:\mathrm{satisfying}\:\mathrm{the} \\ $$$$\mathrm{condition}\:\mathrm{of}\:\mathrm{our}\:\mathrm{problem} \\ $$
Commented by Rasheed.Sindhi last updated on 18/Sep/20
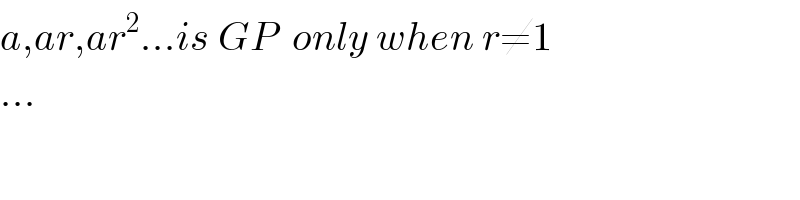
$${a},{ar},{ar}^{\mathrm{2}} …{is}\:{GP}\:\:{only}\:{when}\:{r}\neq\mathrm{1} \\ $$$$… \\ $$
Commented by mr W last updated on 18/Sep/20

$$\mathrm{111} \\ $$$$\mathrm{222} \\ $$$$\mathrm{333} \\ $$$$…. \\ $$$$\mathrm{999} \\ $$$${are}\:{obvious}\:{solutions}. \\ $$
Commented by 1549442205PVT last updated on 18/Sep/20
$$\mathrm{Thank}\:\mathrm{Sir}.\mathrm{I}\:\mathrm{mistaked} \\ $$
Commented by 1549442205PVT last updated on 20/Sep/20
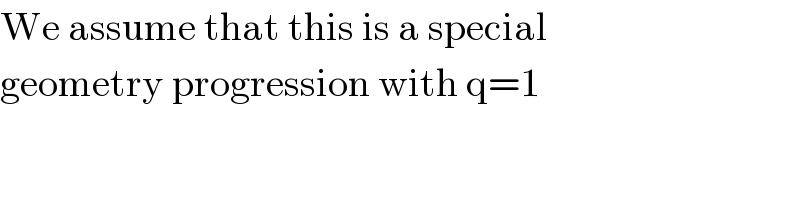
$$\mathrm{We}\:\mathrm{assume}\:\mathrm{that}\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{special} \\ $$$$\mathrm{geometry}\:\mathrm{progression}\:\mathrm{with}\:\mathrm{q}=\mathrm{1} \\ $$
Commented by Rasheed.Sindhi last updated on 20/Sep/20

$${Ok}\:{sir}! \\ $$
