Menu Close

Question-114330

Tinku Tara 0 Comments
Pin




Question Number 114330 by mnjuly1970 last updated on 18/Sep/20
Commented by mnjuly1970 last updated on 18/Sep/20
easy question↑↑↑
$${easy}\:{question}\uparrow\uparrow\uparrow \\ $$
Answered by Dwaipayan Shikari last updated on 18/Sep/20
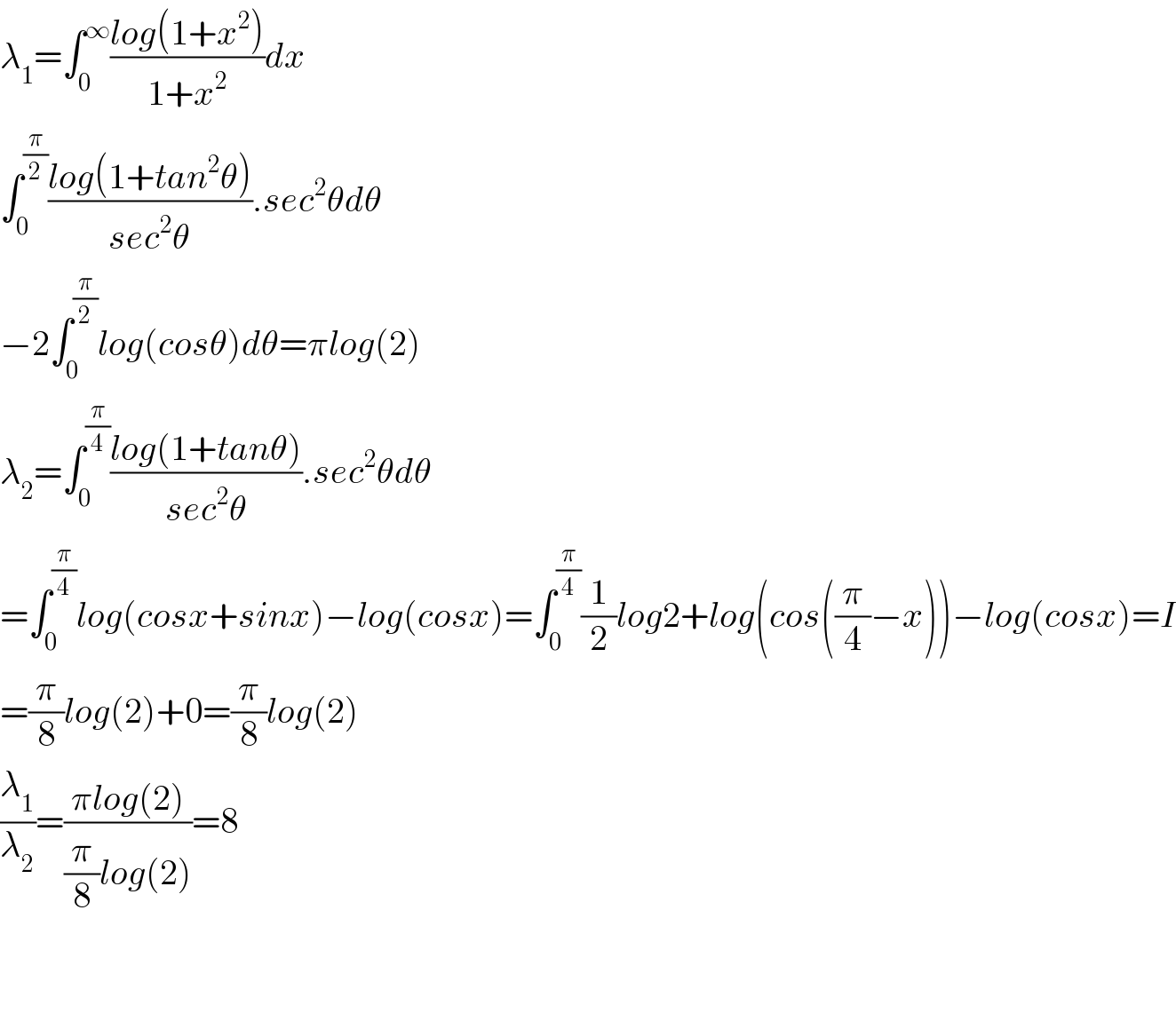
λ_1 =∫_0 ^∞ ((log(1+x^2 ))/(1+x^2 ))dx ∫_0 ^(π/2) ((log(1+tan^2 θ))/(sec^2 θ)).sec^2 θdθ −2∫_0 ^(π/2) log(cosθ)dθ=πlog(2) λ_2 =∫_0 ^(π/4) ((log(1+tanθ))/(sec^2 θ)).sec^2 θdθ =∫_0 ^(π/4) log(cosx+sinx)−log(cosx)=∫_0 ^(π/4) (1/2)log2+log(cos((π/4)−x))−log(cosx)=I =(π/8)log(2)+0=(π/8)log(2) (λ_1 /λ_2 )=((πlog(2))/((π/8)log(2)))=8
$$\lambda_{\mathrm{1}} =\int_{\mathrm{0}} ^{\infty} \frac{{log}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{log}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)}{{sec}^{\mathrm{2}} \theta}.{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({cos}\theta\right){d}\theta=\pi{log}\left(\mathrm{2}\right) \\ $$$$\lambda_{\mathrm{2}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{log}\left(\mathrm{1}+{tan}\theta\right)}{{sec}^{\mathrm{2}} \theta}.{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({cosx}+{sinx}\right)−{log}\left({cosx}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}}{\mathrm{2}}{log}\mathrm{2}+{log}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right)−{log}\left({cosx}\right)={I} \\ $$$$=\frac{\pi}{\mathrm{8}}{log}\left(\mathrm{2}\right)+\mathrm{0}=\frac{\pi}{\mathrm{8}}{log}\left(\mathrm{2}\right) \\ $$$$\frac{\lambda_{\mathrm{1}} }{\lambda_{\mathrm{2}} }=\frac{\pi{log}\left(\mathrm{2}\right)}{\frac{\pi}{\mathrm{8}}{log}\left(\mathrm{2}\right)}=\mathrm{8} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 18/Sep/20
thank you sir .very nice.
$${thank}\:{you}\:{sir}\:.{very}\:{nice}. \\ $$
Answered by mathmax by abdo last updated on 18/Sep/20
we have λ_1 =∫_0 ^∞ ((ln(1+x^2 ))/(1+x^2 ))dx =_(x=tanθ) ∫_0 ^(π/2) ((ln(1+tan^2 θ))/(1+tan^2 θ))(1+tan^2 θ)dθ =∫_0 ^(π/2) ln((1/(cos^2 θ)))dθ =−2∫_0 ^(π/2) ln(cosθ)dθ =−2(−(π/2)ln(2))=πln(2) λ_2 =∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx =_(x=tant) ∫_0 ^(π/4) ((ln(1+tant))/(1+tan^2 t))(1+tan^2 t)dt =∫_0 ^(π/4) ln(1+tant)dt =_(t=(π/4)−u) ∫_0 ^(π/4) ln(1+tan((π/4)−u) du =∫_0 ^(π/4) ln(1+((1−tanu)/(1+tanu)))du =∫_0 ^(π/4) ln( (2/(1+tanu)))du =(π/4)ln(2) −∫_0 ^(π/4) ln(1+tanu)du =(π/4)ln(2)−λ_2 ⇒ 2λ_2 =(π/4)ln(2) ⇒λ_2 =(π/8)ln(2) ⇒(λ_1 /λ_2 ) =((πln(2))/((π/8)ln(2))) ⇒★(λ_1 /λ_2 ) =8 ★
$$\mathrm{we}\:\mathrm{have}\:\lambda_{\mathrm{1}} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\mathrm{tan}\theta} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \theta}\right)\mathrm{d}\theta\:=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{cos}\theta\right)\mathrm{d}\theta\:=−\mathrm{2}\left(−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\right)=\pi\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\lambda_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\mathrm{tant}} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{tant}\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{tant}\right)\mathrm{dt}\:=_{\mathrm{t}=\frac{\pi}{\mathrm{4}}−\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}−\mathrm{u}\right)\:\mathrm{du}\right. \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}−\mathrm{tanu}}{\mathrm{1}+\mathrm{tanu}}\right)\mathrm{du}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\:\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tanu}}\right)\mathrm{du} \\ $$$$=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tanu}\right)\mathrm{du}\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\lambda_{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{2}\lambda_{\mathrm{2}} =\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow\lambda_{\mathrm{2}} =\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow\frac{\lambda_{\mathrm{1}} }{\lambda_{\mathrm{2}} }\:=\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right)}\:\Rightarrow\bigstar\frac{\lambda_{\mathrm{1}} }{\lambda_{\mathrm{2}} }\:=\mathrm{8}\:\bigstar \\ $$
Commented by mnjuly1970 last updated on 18/Sep/20
thank you master (ostad) in our language.very nice.grateful teful
$${thank}\:{you}\:{master}\:\left({ostad}\right)\:{in} \\ $$$${our}\:{language}.{very}\:{nice}.{grateful}\: \\ $$$$ \\ $$$${teful} \\ $$
Commented by mathmax by abdo last updated on 18/Sep/20
you are welcome sir
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *