Question Number 114443 by ARVIND990 last updated on 19/Sep/20

Commented by ARVIND990 last updated on 19/Sep/20

$$\mathrm{fine}\:\mathrm{the}\:\mathrm{projection}\:\mathrm{of}\:\mathrm{point}\:\overset{\rightarrow} {\mathrm{OP}}=\overset{\rightarrow} {\mathrm{p}}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{line}\:\overset{\rightarrow} {\mathrm{r}}=\overset{\rightarrow} {\mathrm{a}}+\lambda\overset{\rightarrow} {\mathrm{b}} \\ $$
Answered by mr W last updated on 19/Sep/20
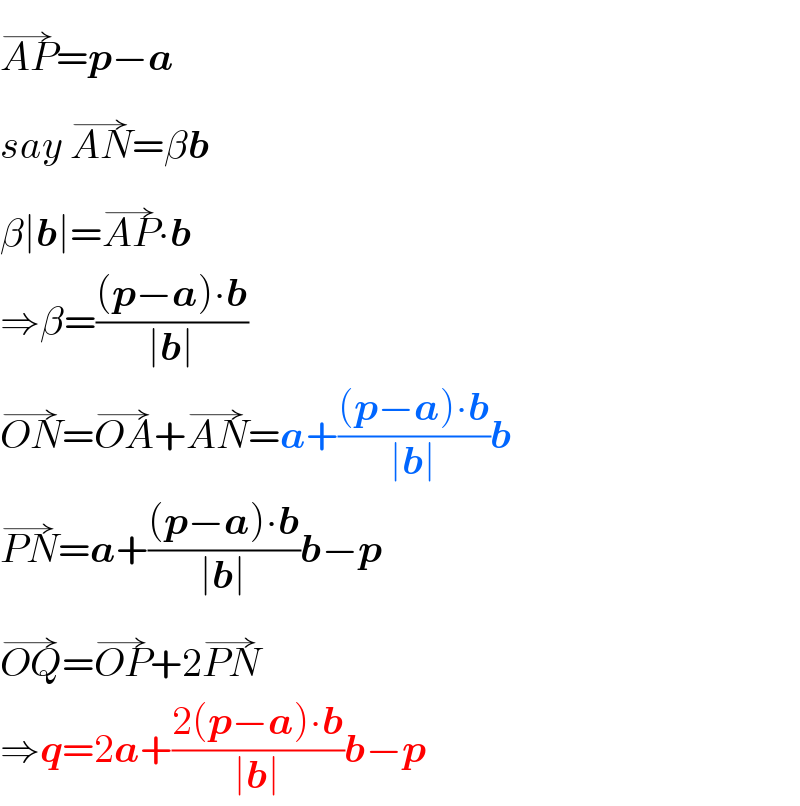
$$\overset{\rightarrow} {{AP}}=\boldsymbol{{p}}−\boldsymbol{{a}} \\ $$$${say}\:\overset{\rightarrow} {{AN}}=\beta\boldsymbol{{b}} \\ $$$$\beta\mid\boldsymbol{{b}}\mid=\overset{\rightarrow} {{AP}}\centerdot\boldsymbol{{b}} \\ $$$$\Rightarrow\beta=\frac{\left(\boldsymbol{{p}}−\boldsymbol{{a}}\right)\centerdot\boldsymbol{{b}}}{\mid\boldsymbol{{b}}\mid} \\ $$$$\overset{\rightarrow} {{ON}}=\overset{\rightarrow} {{OA}}+\overset{\rightarrow} {{AN}}=\boldsymbol{{a}}+\frac{\left(\boldsymbol{{p}}−\boldsymbol{{a}}\right)\centerdot\boldsymbol{{b}}}{\mid\boldsymbol{{b}}\mid}\boldsymbol{{b}} \\ $$$$\overset{\rightarrow} {{PN}}=\boldsymbol{{a}}+\frac{\left(\boldsymbol{{p}}−\boldsymbol{{a}}\right)\centerdot\boldsymbol{{b}}}{\mid\boldsymbol{{b}}\mid}\boldsymbol{{b}}−\boldsymbol{{p}} \\ $$$$\overset{\rightarrow} {{OQ}}=\overset{\rightarrow} {{OP}}+\mathrm{2}\overset{\rightarrow} {{PN}} \\ $$$$\Rightarrow\boldsymbol{{q}}=\mathrm{2}\boldsymbol{{a}}+\frac{\mathrm{2}\left(\boldsymbol{{p}}−\boldsymbol{{a}}\right)\centerdot\boldsymbol{{b}}}{\mid\boldsymbol{{b}}\mid}\boldsymbol{{b}}−\boldsymbol{{p}} \\ $$
Commented by ARVIND990 last updated on 19/Sep/20

$$\mathrm{i}\:\mathrm{dont}\:\mathrm{understand}\:\mathrm{pls}\:\mathrm{make}\:\mathrm{a}\:\mathrm{yours}\: \\ $$$$\mathrm{digram}\:\mathrm{and}\:\mathrm{deep}\:\mathrm{solution}\:\mathrm{like}\:\mathrm{how}\: \\ $$$$\mathrm{AP}=\mathrm{p}−\mathrm{a}\:\mathrm{pls} \\ $$
Commented by ARVIND990 last updated on 19/Sep/20

$$\mathrm{and}\:\mathrm{my}\:\mathrm{question}\:\mathrm{is}\:\mathrm{projection}\:\mathrm{of}\:\overset{\rightarrow} {\mathrm{OP}}\: \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mid\overset{\rightarrow} {\mathrm{OP}}\mid\mathrm{cos}\theta\:\mathrm{maybe} \\ $$
Commented by ARVIND990 last updated on 19/Sep/20

$$\mid\overset{\rightarrow} {\mathrm{OP}}\mid\mathrm{cos}\theta\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\frac{\overset{\rightarrow} {\mathrm{r}}.\overset{\rightarrow} {\mathrm{p}}}{\mid\overset{\rightarrow} {\mathrm{r}}\mid}\:=\overset{\rightarrow} {\mathrm{p}}.\hat {\mathrm{r}} \\ $$
Commented by ARVIND990 last updated on 19/Sep/20

$$\mathrm{and}\:\mathrm{pls}\:\mathrm{show}\:\overset{\rightarrow} {\mathrm{r}}\:\mathrm{in}\:\mathrm{daigram}\: \\ $$
Commented by mr W last updated on 19/Sep/20

$$\overset{\rightarrow} {{OA}}+\overset{\rightarrow} {{AP}}=\overset{\rightarrow} {{OP}} \\ $$$$\boldsymbol{{a}}+\overset{\rightarrow} {{AP}}=\boldsymbol{{p}} \\ $$$$\Rightarrow\overset{\rightarrow} {{AP}}=\boldsymbol{{p}}−\boldsymbol{{a}} \\ $$
Commented by mr W last updated on 19/Sep/20

$${your}\:{question}\:{is}\:{about}\:{the}\:{projection} \\ $$$${of}\:{point}\:{P}\:\:{in}\:{line}\:\boldsymbol{{a}}+\lambda\boldsymbol{{b}},\:{that}\:{is}\:{the} \\ $$$${point}\:{N},\:{which}\:{is}\:{given}\:{by} \\ $$$$\overset{\rightarrow} {{ON}}=\boldsymbol{{a}}+\frac{\left(\boldsymbol{{p}}−\boldsymbol{{a}}\right)\centerdot\boldsymbol{{b}}}{\mid\boldsymbol{{b}}\mid}\boldsymbol{{b}} \\ $$$${Q}\:{is}\:{the}\:{image}\:{of}\:{point}\:{P}\:{in}\:{the}\:{line} \\ $$$$\boldsymbol{{a}}+\lambda\boldsymbol{{b}}. \\ $$
Commented by mr W last updated on 19/Sep/20

$$\boldsymbol{{r}}=\boldsymbol{{a}}+\lambda\boldsymbol{{b}} \\ $$$$\left(−\infty<\lambda<+\infty\right) \\ $$$${which}\:{is}\:{the}\:{line}\:{in}\:{your}\:{diagram} \\ $$$${where}\:{the}\:{vector}\:\boldsymbol{{b}}\:{is}\:{shown}. \\ $$
Commented by mr W last updated on 19/Sep/20

