Question Number 114480 by mohammad17 last updated on 19/Sep/20

Commented by mohammad17 last updated on 19/Sep/20

$${help}\:{me}\:{sir} \\ $$
Answered by john santu last updated on 19/Sep/20

$$\left(\mathrm{4}\right)\:\mathrm{2}{y}+{x}\:=\:\mathrm{2}\left(−\mathrm{1}\right)+\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}{y}+{x}\:=\:\mathrm{0}\:;\:{y}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}{x} \\ $$$$\left(\mathrm{5}\right)\:\mathrm{8}{x}−{y}=\mathrm{8}\left(\mathrm{7}\right)−\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{8}{x}−{y}\:=\:\mathrm{55}\:;\:{y}\:=\:\mathrm{8}{x}−\mathrm{55} \\ $$
Commented by mohammad17 last updated on 19/Sep/20

$${thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 19/Sep/20
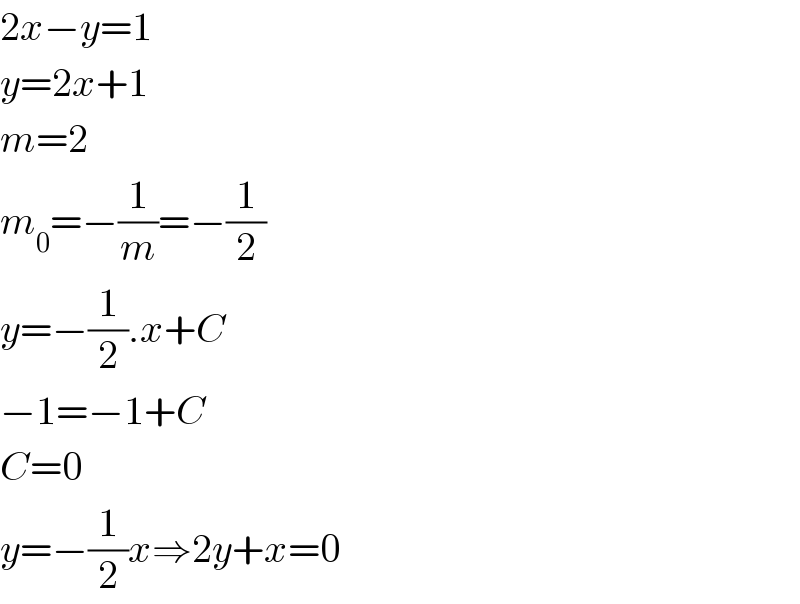
$$\mathrm{2}{x}−{y}=\mathrm{1} \\ $$$${y}=\mathrm{2}{x}+\mathrm{1} \\ $$$${m}=\mathrm{2} \\ $$$${m}_{\mathrm{0}} =−\frac{\mathrm{1}}{{m}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}=−\frac{\mathrm{1}}{\mathrm{2}}.{x}+{C} \\ $$$$−\mathrm{1}=−\mathrm{1}+{C} \\ $$$${C}=\mathrm{0} \\ $$$${y}=−\frac{\mathrm{1}}{\mathrm{2}}{x}\Rightarrow\mathrm{2}{y}+{x}=\mathrm{0} \\ $$
Commented by mohammad17 last updated on 19/Sep/20

$${thank}\:{you}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 19/Sep/20
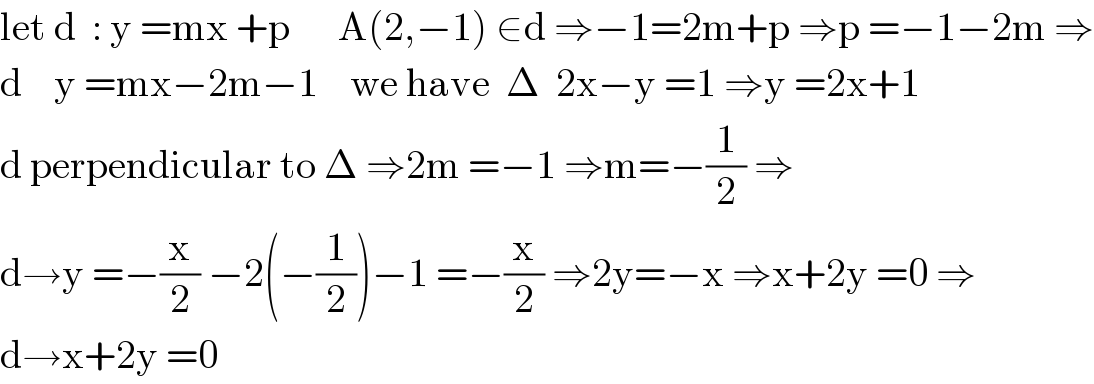
$$\mathrm{let}\:\mathrm{d}\:\::\:\mathrm{y}\:=\mathrm{mx}\:+\mathrm{p}\:\:\:\:\:\:\mathrm{A}\left(\mathrm{2},−\mathrm{1}\right)\:\in\mathrm{d}\:\Rightarrow−\mathrm{1}=\mathrm{2m}+\mathrm{p}\:\Rightarrow\mathrm{p}\:=−\mathrm{1}−\mathrm{2m}\:\Rightarrow \\ $$$$\mathrm{d}\:\:\:\:\mathrm{y}\:=\mathrm{mx}−\mathrm{2m}−\mathrm{1}\:\:\:\:\mathrm{we}\:\mathrm{have}\:\:\Delta\:\:\mathrm{2x}−\mathrm{y}\:=\mathrm{1}\:\Rightarrow\mathrm{y}\:=\mathrm{2x}+\mathrm{1} \\ $$$$\mathrm{d}\:\mathrm{perpendicular}\:\mathrm{to}\:\Delta\:\Rightarrow\mathrm{2m}\:=−\mathrm{1}\:\Rightarrow\mathrm{m}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{d}\rightarrow\mathrm{y}\:=−\frac{\mathrm{x}}{\mathrm{2}}\:−\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}\:=−\frac{\mathrm{x}}{\mathrm{2}}\:\Rightarrow\mathrm{2y}=−\mathrm{x}\:\Rightarrow\mathrm{x}+\mathrm{2y}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{d}\rightarrow\mathrm{x}+\mathrm{2y}\:=\mathrm{0} \\ $$
