Question-114485

Question Number 114485 by mohammad17 last updated on 19/Sep/20

Answered by Dwaipayan Shikari last updated on 19/Sep/20

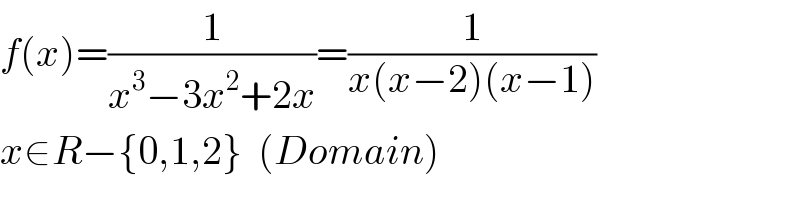
f(x)=(1/(x^3 −3x^2 +2x))=(1/(x(x−2)(x−1))) x∈R−{0,1,2} (Domain)

$${f}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}}=\frac{\mathrm{1}}{{x}\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)} \\ $$$${x}\in{R}−\left\{\mathrm{0},\mathrm{1},\mathrm{2}\right\}\:\:\left({Domain}\right) \\ $$

Commented by mohammad17 last updated on 19/Sep/20

$${thank}\:{you}\:{sir} \\ $$

Answered by Dwaipayan Shikari last updated on 19/Sep/20

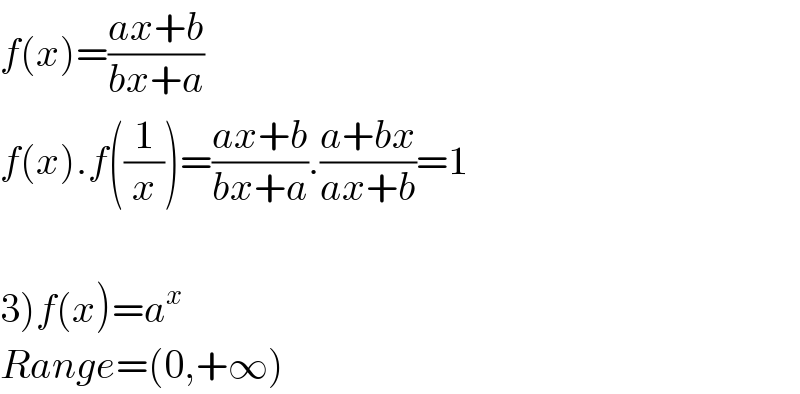
f(x)=((ax+b)/(bx+a)) f(x).f((1/x))=((ax+b)/(bx+a)).((a+bx)/(ax+b))=1 3)f(x)=a^x Range=(0,+∞)

$${f}\left({x}\right)=\frac{{ax}+{b}}{{bx}+{a}} \\ $$$${f}\left({x}\right).{f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{{ax}+{b}}{{bx}+{a}}.\frac{{a}+{bx}}{{ax}+{b}}=\mathrm{1} \\ $$$$ \\ $$$$\left.\mathrm{3}\right){f}\left({x}\right)={a}^{{x}} \\ $$$${Range}=\left(\mathrm{0},+\infty\right) \\ $$

Commented by mohammad17 last updated on 19/Sep/20

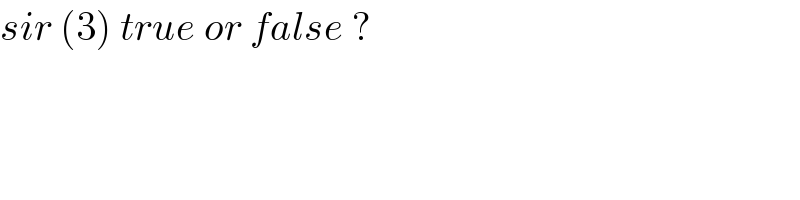
$${sir}\:\left(\mathrm{3}\right)\:{true}\:{or}\:{false}\:? \\ $$

Answered by 1549442205PVT last updated on 19/Sep/20

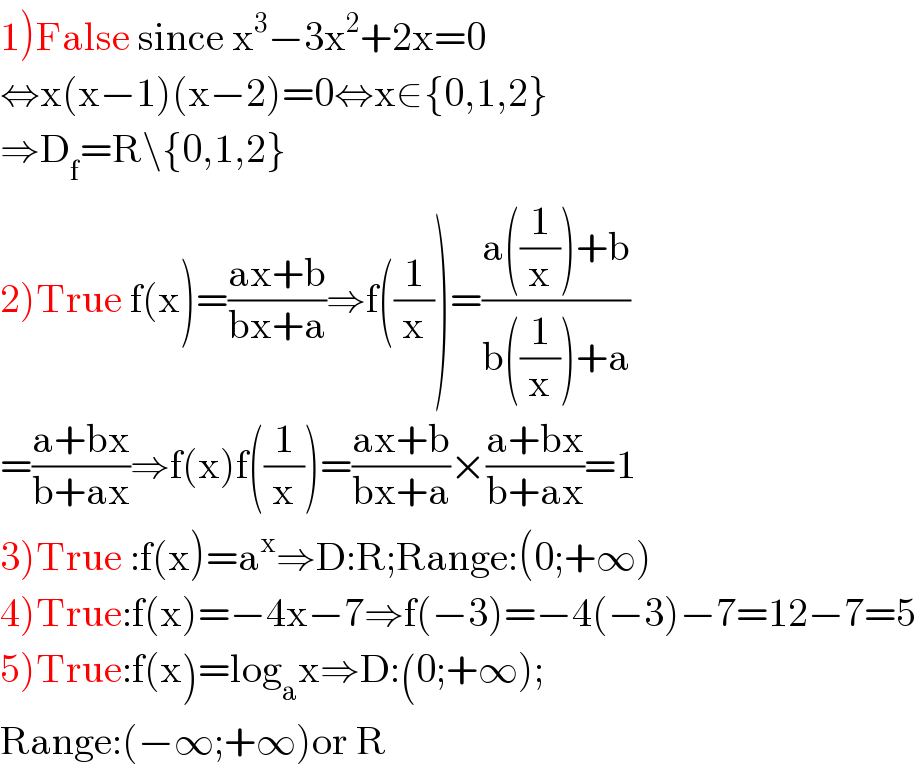
1)False since x^3 −3x^2 +2x=0 ⇔x(x−1)(x−2)=0⇔x∈{0,1,2} ⇒D_f =R\{0,1,2} 2)True f(x)=((ax+b)/(bx+a))⇒f((1/x))=((a((1/x))+b)/(b((1/x))+a)) =((a+bx)/(b+ax))⇒f(x)f((1/x))=((ax+b)/(bx+a))×((a+bx)/(b+ax))=1 3)True :f(x)=a^x ⇒D:R;Range:(0;+∞) 4)True:f(x)=−4x−7⇒f(−3)=−4(−3)−7=12−7=5 5)True:f(x)=log_a x⇒D:(0;+∞); Range:(−∞;+∞)or R

$$\left.\mathrm{1}\right)\mathrm{False}\:\mathrm{since}\:\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)=\mathrm{0}\Leftrightarrow\mathrm{x}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2}\right\} \\ $$$$\Rightarrow\mathrm{D}_{\mathrm{f}} =\mathrm{R}\backslash\left\{\mathrm{0},\mathrm{1},\mathrm{2}\right\} \\ $$$$\left.\mathrm{2}\right)\mathrm{True}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{bx}+\mathrm{a}}\Rightarrow\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{a}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{b}}{\mathrm{b}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{a}} \\ $$$$=\frac{\mathrm{a}+\mathrm{bx}}{\mathrm{b}+\mathrm{ax}}\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{bx}+\mathrm{a}}×\frac{\mathrm{a}+\mathrm{bx}}{\mathrm{b}+\mathrm{ax}}=\mathrm{1} \\ $$$$\left.\mathrm{3}\right)\mathrm{True}\::\mathrm{f}\left(\mathrm{x}\right)=\mathrm{a}^{\mathrm{x}} \Rightarrow\mathrm{D}:\mathrm{R};\mathrm{Range}:\left(\mathrm{0};+\infty\right) \\ $$$$\left.\mathrm{4}\right)\mathrm{True}:\mathrm{f}\left(\mathrm{x}\right)=−\mathrm{4x}−\mathrm{7}\Rightarrow\mathrm{f}\left(−\mathrm{3}\right)=−\mathrm{4}\left(−\mathrm{3}\right)−\mathrm{7}=\mathrm{12}−\mathrm{7}=\mathrm{5} \\ $$$$\left.\mathrm{5}\right)\mathrm{True}:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{log}_{\mathrm{a}} \mathrm{x}\Rightarrow\mathrm{D}:\left(\mathrm{0};+\infty\right); \\ $$$$\mathrm{Range}:\left(−\infty;+\infty\right)\mathrm{or}\:\mathrm{R} \\ $$

Commented by mohammad17 last updated on 19/Sep/20

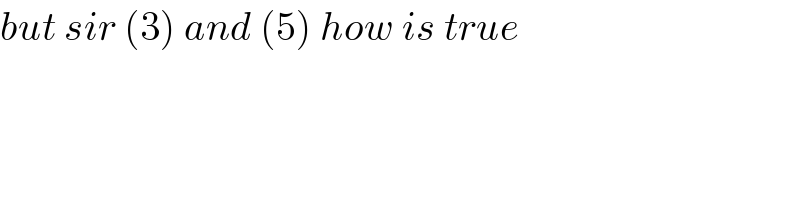
$${but}\:{sir}\:\left(\mathrm{3}\right)\:{and}\:\left(\mathrm{5}\right)\:{how}\:{is}\:{true} \\ $$

Commented by mohammad17 last updated on 19/Sep/20

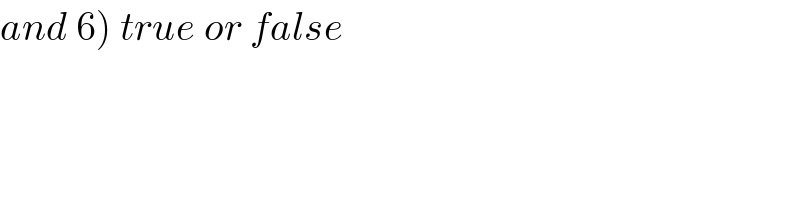
$$\left.{and}\:\mathrm{6}\right)\:{true}\:{or}\:{false} \\ $$

Commented by 1549442205PVT last updated on 19/Sep/20

$$\mathrm{available}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{true} \\ $$

Commented by 1549442205PVT last updated on 19/Sep/20

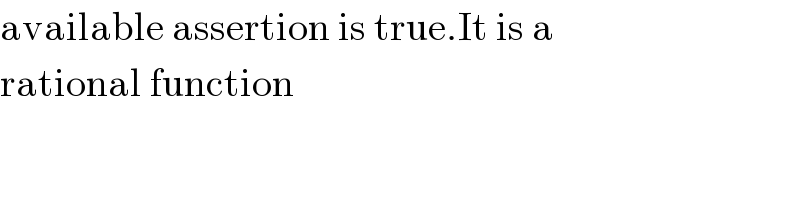
available assertion is true.It is a rational function

$$\mathrm{available}\:\mathrm{assertion}\:\mathrm{is}\:\mathrm{true}.\mathrm{It}\:\mathrm{is}\:\mathrm{a} \\ $$$$\mathrm{rational}\:\mathrm{function} \\ $$

Commented by PRITHWISH SEN 2 last updated on 19/Sep/20

I think there should be a restriction on 6 and it is ∣x∣≠2

$$\mathrm{I}\:\mathrm{think}\:\mathrm{there}\:\mathrm{should}\:\mathrm{be}\:\mathrm{a}\:\mathrm{restriction}\:\mathrm{on}\:\mathrm{6}\:\mathrm{and}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mid\boldsymbol{\mathrm{x}}\mid\neq\mathrm{2} \\ $$

Commented by Aziztisffola last updated on 20/Sep/20

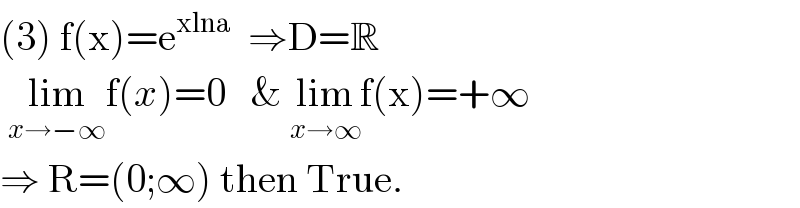
(3) f(x)=e^(xlna) ⇒D=R lim_(x→−∞) f(x)=0 & lim_(x→∞) f(x)=+∞ ⇒ R=(0;∞) then True.

$$\left(\mathrm{3}\right)\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{xlna}} \:\:\Rightarrow\mathrm{D}=\mathbb{R}\: \\ $$$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}f}\left({x}\right)=\mathrm{0}\:\:\:\&\:\underset{{x}\rightarrow\infty} {\mathrm{lim}f}\left(\mathrm{x}\right)=+\infty \\ $$$$\Rightarrow\:\mathrm{R}=\left(\mathrm{0};\infty\right)\:\mathrm{then}\:\mathrm{True}. \\ $$

Commented by 1549442205PVT last updated on 20/Sep/20

Question 6 don′t require to find domain but to assert the true or the false

$$\mathrm{Question}\:\mathrm{6}\:\mathrm{don}'\mathrm{t}\:\mathrm{require}\:\mathrm{to}\:\mathrm{find}\:\mathrm{domain} \\ $$$$\mathrm{but}\:\mathrm{to}\:\mathrm{assert}\:\mathrm{the}\:\mathrm{true}\:\mathrm{or}\:\mathrm{the}\:\mathrm{false} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply