Menu Close

Question-114533

Tinku Tara 0 Comments
Pin




Question Number 114533 by 675480065 last updated on 19/Sep/20
Answered by abdomsup last updated on 19/Sep/20
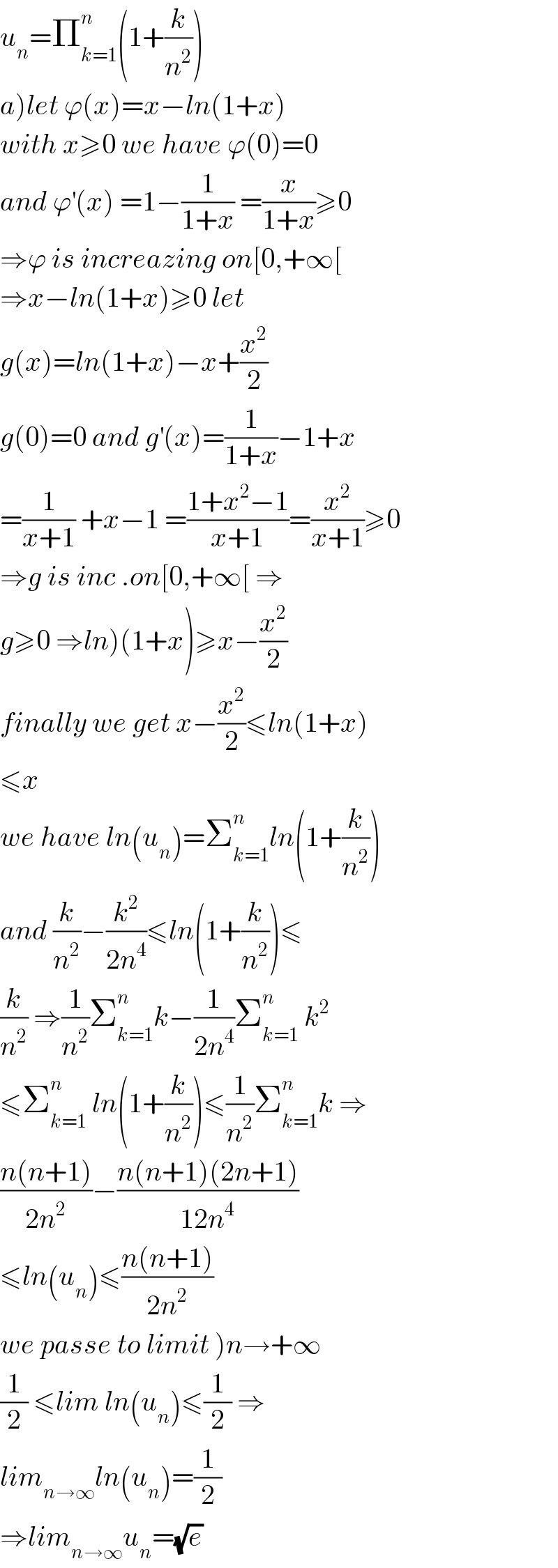
u_n =Π_(k=1) ^n (1+(k/n^2 )) a)let ϕ(x)=x−ln(1+x) with x≥0 we have ϕ(0)=0 and ϕ^′ (x) =1−(1/(1+x)) =(x/(1+x))≥0 ⇒ϕ is increazing on[0,+∞[ ⇒x−ln(1+x)≥0 let g(x)=ln(1+x)−x+(x^2 /2) g(0)=0 and g^′ (x)=(1/(1+x))−1+x =(1/(x+1)) +x−1 =((1+x^2 −1)/(x+1))=(x^2 /(x+1))≥0 ⇒g is inc .on[0,+∞[ ⇒ g≥0 ⇒ln)(1+x)≥x−(x^2 /2) finally we get x−(x^2 /2)≤ln(1+x) ≤x we have ln(u_n )=Σ_(k=1) ^n ln(1+(k/n^2 )) and (k/n^2 )−(k^2 /(2n^4 ))≤ln(1+(k/n^2 ))≤ (k/n^2 ) ⇒(1/n^2 )Σ_(k=1) ^n k−(1/(2n^4 ))Σ_(k=1) ^n k^2 ≤Σ_(k=1) ^n ln(1+(k/n^2 ))≤(1/n^2 )Σ_(k=1) ^n k ⇒ ((n(n+1))/(2n^2 ))−((n(n+1)(2n+1))/(12n^4 )) ≤ln(u_n )≤((n(n+1))/(2n^2 )) we passe to limit )n→+∞ (1/2) ≤lim ln(u_n )≤(1/2) ⇒ lim_(n→∞) ln(u_n )=(1/2) ⇒lim_(n→∞) u_n =(√e)
$${u}_{{n}} =\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right) \\ $$$$\left.{a}\right){let}\:\varphi\left({x}\right)={x}−{ln}\left(\mathrm{1}+{x}\right) \\ $$$${with}\:{x}\geqslant\mathrm{0}\:{we}\:{have}\:\varphi\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${and}\:\varphi^{'} \left({x}\right)\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\frac{{x}}{\mathrm{1}+{x}}\geqslant\mathrm{0} \\ $$$$\Rightarrow\varphi\:{is}\:{increazing}\:{on}\left[\mathrm{0},+\infty\left[\right.\right. \\ $$$$\Rightarrow{x}−{ln}\left(\mathrm{1}+{x}\right)\geqslant\mathrm{0}\:{let} \\ $$$${g}\left({x}\right)={ln}\left(\mathrm{1}+{x}\right)−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${g}\left(\mathrm{0}\right)=\mathrm{0}\:{and}\:{g}^{'} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}}−\mathrm{1}+{x} \\ $$$$=\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+{x}−\mathrm{1}\:=\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{{x}+\mathrm{1}}=\frac{{x}^{\mathrm{2}} }{{x}+\mathrm{1}}\geqslant\mathrm{0} \\ $$$$\Rightarrow{g}\:{is}\:{inc}\:.{on}\left[\mathrm{0},+\infty\left[\:\Rightarrow\right.\right. \\ $$$$\left.{g}\geqslant\mathrm{0}\:\Rightarrow{ln}\right)\left(\mathrm{1}+{x}\right)\geqslant{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${finally}\:{we}\:{get}\:{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\leqslant{ln}\left(\mathrm{1}+{x}\right) \\ $$$$\leqslant{x} \\ $$$${we}\:{have}\:{ln}\left({u}_{{n}} \right)=\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right) \\ $$$${and}\:\frac{{k}}{{n}^{\mathrm{2}} }−\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\leqslant{ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\leqslant \\ $$$$\frac{{k}}{{n}^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{n}} {k}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{4}} }\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}} \\ $$$$\leqslant\sum_{{k}=\mathrm{1}} ^{{n}} \:{ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{n}} {k}\:\Rightarrow \\ $$$$\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }−\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}{n}^{\mathrm{4}} } \\ $$$$\leqslant{ln}\left({u}_{{n}} \right)\leqslant\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} } \\ $$$$\left.{we}\:{passe}\:{to}\:{limit}\:\right){n}\rightarrow+\infty \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\leqslant{lim}\:{ln}\left({u}_{{n}} \right)\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow\infty} {ln}\left({u}_{{n}} \right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{lim}_{{n}\rightarrow\infty} {u}_{{n}} =\sqrt{{e}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *