Question Number 114561 by Akeyz last updated on 19/Sep/20

Answered by bemath last updated on 19/Sep/20
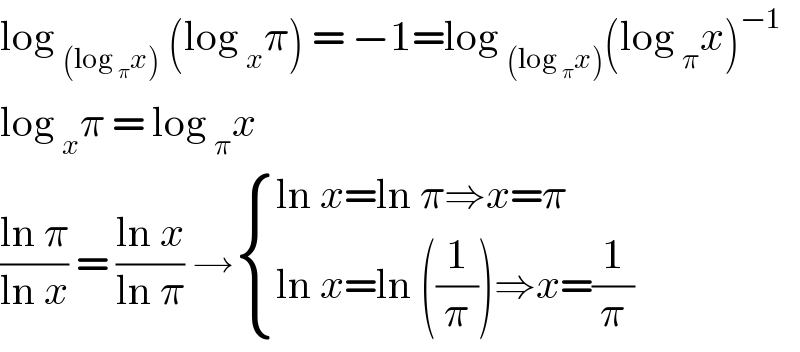
$$\mathrm{log}\:_{\left(\mathrm{log}\:_{\pi} {x}\right)} \:\left(\mathrm{log}\:_{{x}} \pi\right)\:=\:−\mathrm{1}=\mathrm{log}\:_{\left(\mathrm{log}\:_{\pi} {x}\right)} \left(\mathrm{log}\:_{\pi} {x}\right)^{−\mathrm{1}} \\ $$$$\mathrm{log}\:_{{x}} \pi\:=\:\mathrm{log}\:_{\pi} {x}\: \\ $$$$\frac{\mathrm{ln}\:\pi}{\mathrm{ln}\:{x}}\:=\:\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\pi}\:\rightarrow\begin{cases}{\mathrm{ln}\:{x}=\mathrm{ln}\:\pi\Rightarrow{x}=\pi}\\{\mathrm{ln}\:{x}=\mathrm{ln}\:\left(\frac{\mathrm{1}}{\pi}\right)\Rightarrow{x}=\frac{\mathrm{1}}{\pi}}\end{cases} \\ $$
