Question Number 114615 by I want to learn more last updated on 19/Sep/20

Answered by Olaf last updated on 19/Sep/20
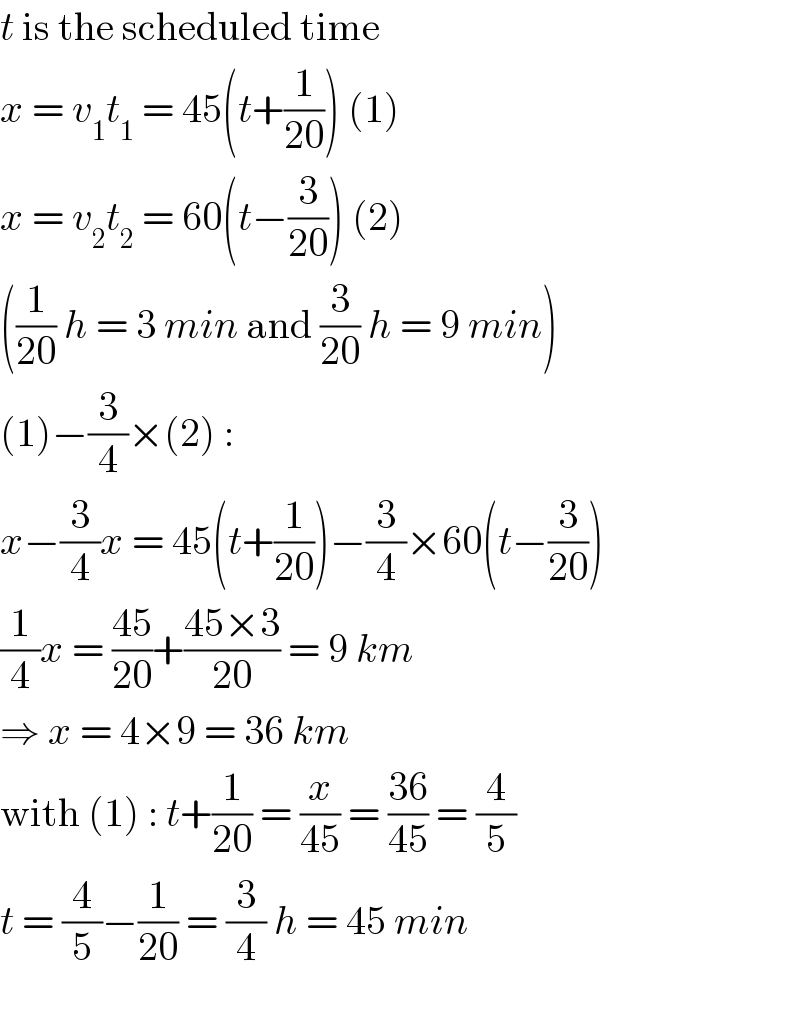
$${t}\:\mathrm{is}\:\mathrm{the}\:\mathrm{scheduled}\:\mathrm{time} \\ $$$${x}\:=\:{v}_{\mathrm{1}} {t}_{\mathrm{1}} \:=\:\mathrm{45}\left({t}+\frac{\mathrm{1}}{\mathrm{20}}\right)\:\left(\mathrm{1}\right) \\ $$$${x}\:=\:{v}_{\mathrm{2}} {t}_{\mathrm{2}} \:=\:\mathrm{60}\left({t}−\frac{\mathrm{3}}{\mathrm{20}}\right)\:\left(\mathrm{2}\right) \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{20}}\:{h}\:=\:\mathrm{3}\:{min}\:\mathrm{and}\:\frac{\mathrm{3}}{\mathrm{20}}\:{h}\:=\:\mathrm{9}\:{min}\right) \\ $$$$\left(\mathrm{1}\right)−\frac{\mathrm{3}}{\mathrm{4}}×\left(\mathrm{2}\right)\:: \\ $$$${x}−\frac{\mathrm{3}}{\mathrm{4}}{x}\:=\:\mathrm{45}\left({t}+\frac{\mathrm{1}}{\mathrm{20}}\right)−\frac{\mathrm{3}}{\mathrm{4}}×\mathrm{60}\left({t}−\frac{\mathrm{3}}{\mathrm{20}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{x}\:=\:\frac{\mathrm{45}}{\mathrm{20}}+\frac{\mathrm{45}×\mathrm{3}}{\mathrm{20}}\:=\:\mathrm{9}\:{km} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{4}×\mathrm{9}\:=\:\mathrm{36}\:{km} \\ $$$$\mathrm{with}\:\left(\mathrm{1}\right)\::\:{t}+\frac{\mathrm{1}}{\mathrm{20}}\:=\:\frac{{x}}{\mathrm{45}}\:=\:\frac{\mathrm{36}}{\mathrm{45}}\:=\:\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${t}\:=\:\frac{\mathrm{4}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{20}}\:=\:\frac{\mathrm{3}}{\mathrm{4}}\:{h}\:=\:\mathrm{45}\:{min} \\ $$$$ \\ $$
Commented by I want to learn more last updated on 20/Sep/20
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate} \\ $$
