Question Number 114625 by bobhans last updated on 20/Sep/20
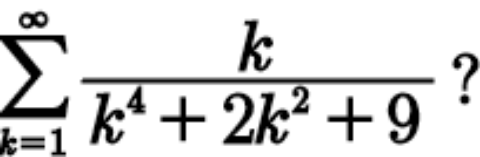
Answered by john santu last updated on 20/Sep/20
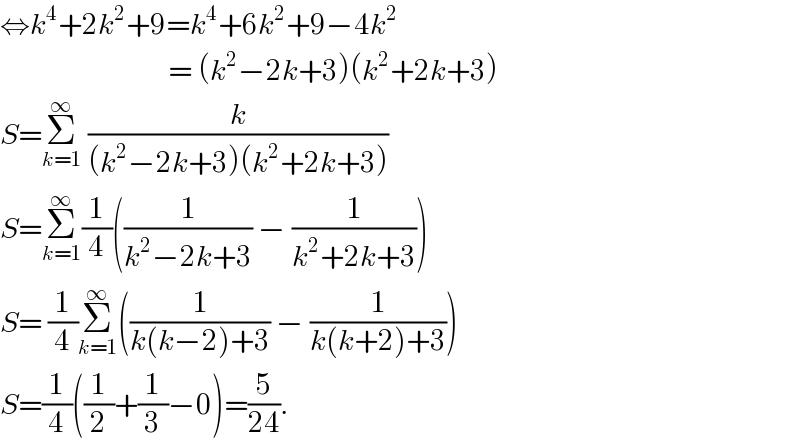
$$\Leftrightarrow{k}^{\mathrm{4}} +\mathrm{2}{k}^{\mathrm{2}} +\mathrm{9}={k}^{\mathrm{4}} +\mathrm{6}{k}^{\mathrm{2}} +\mathrm{9}−\mathrm{4}{k}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left({k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{3}\right)\left({k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{3}\right) \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{k}}{\left({k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{3}\right)\left({k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{3}\right)} \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{3}}\:−\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{3}}\right) \\ $$$${S}=\:\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}\left({k}−\mathrm{2}\right)+\mathrm{3}}\:−\:\frac{\mathrm{1}}{{k}\left({k}+\mathrm{2}\right)+\mathrm{3}}\right) \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{0}\right)=\frac{\mathrm{5}}{\mathrm{24}}. \\ $$
Commented by bobhans last updated on 20/Sep/20

$${gives}\:“{like}“ \\ $$
