Question Number 114682 by 175mohamed last updated on 20/Sep/20
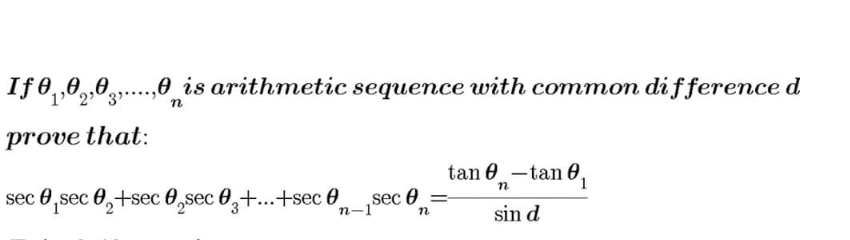
Answered by mindispower last updated on 20/Sep/20
![∀k∈[2,n] tg(a_k )−tg(a_(k−1) )=((sin(a_k ))/(cos(a_k )))−((sin(a_(k−1) ))/(cos(a_(k−1) ))) =sin(a_k −a_(k−1) )sec(a_k )sec(a_(k−1) ) =sin(d)sec(a_k )sec(a_(k−1) ) ⇔((tg(a_k )−tg(a_(k−1) ))/(sin(d)))=sec(a_k )sec(a_(k−1) ) Σ_(k=2) ^n ((tg(a_k )−tg(a_(k−1) ))/(sin(d)))=Σ_(k=2) ^n sec(a_k )sec(a_(k−1) ) ⇔((tg(a_n )−tg(a_1 ))/(sin(d)))=sec(a_1 )sec(a_2 )+ sec(a_2 )sec(a_3 )+...+sec(a_(n−1) )sec(a_n )](https://www.tinkutara.com/question/Q114724.png)
$$\forall{k}\in\left[\mathrm{2},{n}\right] \\ $$$${tg}\left({a}_{{k}} \right)−{tg}\left({a}_{{k}−\mathrm{1}} \right)=\frac{{sin}\left({a}_{{k}} \right)}{{cos}\left({a}_{{k}} \right)}−\frac{{sin}\left({a}_{{k}−\mathrm{1}} \right)}{{cos}\left({a}_{{k}−\mathrm{1}} \right)} \\ $$$$={sin}\left({a}_{{k}} −{a}_{{k}−\mathrm{1}} \right){sec}\left({a}_{{k}} \right){sec}\left({a}_{{k}−\mathrm{1}} \right) \\ $$$$={sin}\left({d}\right){sec}\left({a}_{{k}} \right){sec}\left({a}_{{k}−\mathrm{1}} \right) \\ $$$$\Leftrightarrow\frac{{tg}\left({a}_{{k}} \right)−{tg}\left({a}_{{k}−\mathrm{1}} \right)}{{sin}\left({d}\right)}={sec}\left({a}_{{k}} \right){sec}\left({a}_{{k}−\mathrm{1}} \right) \\ $$$$\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\frac{{tg}\left({a}_{{k}} \right)−{tg}\left({a}_{{k}−\mathrm{1}} \right)}{{sin}\left({d}\right)}=\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}{sec}\left({a}_{{k}} \right){sec}\left({a}_{{k}−\mathrm{1}} \right) \\ $$$$\Leftrightarrow\frac{{tg}\left({a}_{{n}} \right)−{tg}\left({a}_{\mathrm{1}} \right)}{{sin}\left({d}\right)}={sec}\left({a}_{\mathrm{1}} \right){sec}\left({a}_{\mathrm{2}} \right)+ \\ $$$${sec}\left({a}_{\mathrm{2}} \right){sec}\left({a}_{\mathrm{3}} \right)+…+{sec}\left({a}_{{n}−\mathrm{1}} \right){sec}\left({a}_{{n}} \right) \\ $$
