Question Number 114720 by Algoritm last updated on 20/Sep/20
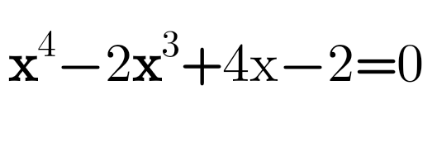
Answered by 1549442205PVT last updated on 20/Sep/20
![x^4 −2x^3 +4x−2⇔(x^2 −x+1)^2 −3x^2 +6x−3=0 ⇔(x^2 −x+1)^2 −3(x−1)^2 =0 ⇔[x^2 +((√3)−1)x+1−(√3)][x^2 −(1+(√3))x+1+(√3)]=0 i)⇔x^2 +((√3)−1)x+1−(√3)=0 Δ=((√3)−1)^2 +4((√3)−1)=2(√3) x=((1−(√3)±(√(2(√3))))/2) ii)x^2 −(1+(√3))x+1+(√3)=0 Δ=(1+(√3))^2 −4(1+(√3))=−2(√3)<0 ⇒has no roots Thus,the given equation has two roots x∈{((1−(√3)+(√(2(√3))))/2),((1−(√3)−(√(2(√3))))/2)}](https://www.tinkutara.com/question/Q114723.png)
$$\mathrm{x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{3}} +\mathrm{4x}−\mathrm{2}\Leftrightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{3}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Leftrightarrow\left[\mathrm{x}^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\mathrm{x}+\mathrm{1}−\sqrt{\mathrm{3}}\right]\left[\mathrm{x}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\mathrm{x}+\mathrm{1}+\sqrt{\mathrm{3}}\right]=\mathrm{0} \\ $$$$\left.\mathrm{i}\right)\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\mathrm{x}+\mathrm{1}−\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\Delta=\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\mathrm{x}=\frac{\mathrm{1}−\sqrt{\mathrm{3}}\pm\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$$\left.\mathrm{ii}\right)\mathrm{x}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\mathrm{x}+\mathrm{1}+\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)=−\mathrm{2}\sqrt{\mathrm{3}}<\mathrm{0} \\ $$$$\Rightarrow\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{two} \\ $$$$\mathrm{roots}\:\mathrm{x}\in\left\{\frac{\mathrm{1}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{2}},\frac{\mathrm{1}−\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{2}}\right\} \\ $$
Answered by MJS_new last updated on 20/Sep/20
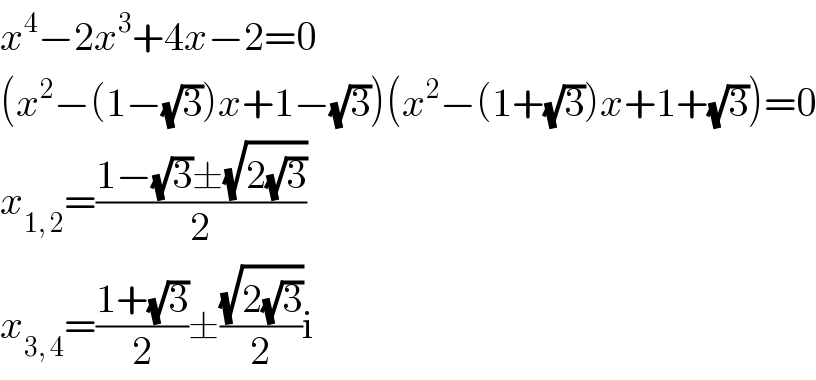
$${x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{4}{x}−\mathrm{2}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){x}+\mathrm{1}−\sqrt{\mathrm{3}}\right)\left({x}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){x}+\mathrm{1}+\sqrt{\mathrm{3}}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1},\:\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{3}}\pm\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} =\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{2}}\mathrm{i} \\ $$
