Question Number 114800 by mohammad17 last updated on 21/Sep/20

Commented by mohammad17 last updated on 21/Sep/20

$${hrlp}\:{me}\:{sir} \\ $$
Commented by mohammad17 last updated on 21/Sep/20

Commented by mohammad17 last updated on 21/Sep/20

Answered by Dwaipayan Shikari last updated on 21/Sep/20
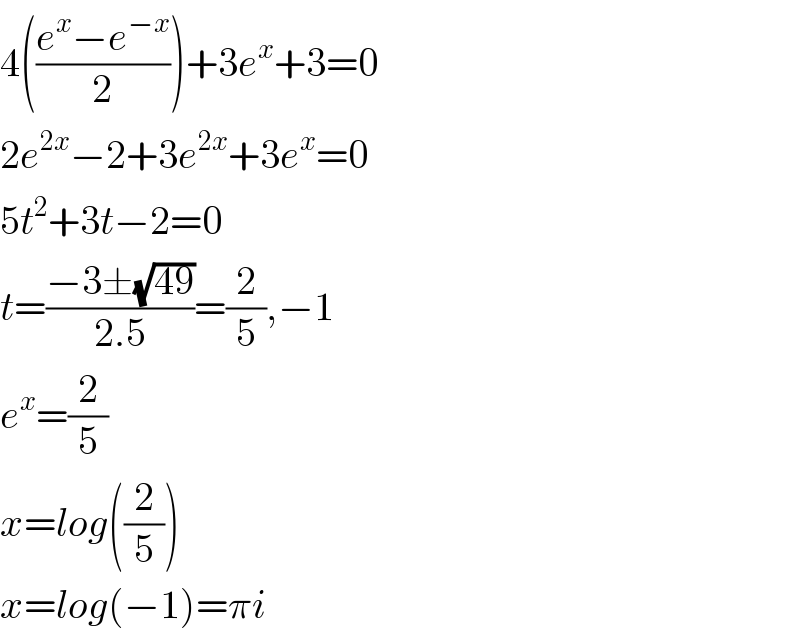
$$\mathrm{4}\left(\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}}\right)+\mathrm{3}{e}^{{x}} +\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{2}{e}^{\mathrm{2}{x}} −\mathrm{2}+\mathrm{3}{e}^{\mathrm{2}{x}} +\mathrm{3}{e}^{{x}} =\mathrm{0} \\ $$$$\mathrm{5}{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{2}=\mathrm{0} \\ $$$${t}=\frac{−\mathrm{3}\pm\sqrt{\mathrm{49}}}{\mathrm{2}.\mathrm{5}}=\frac{\mathrm{2}}{\mathrm{5}},−\mathrm{1} \\ $$$${e}^{{x}} =\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${x}={log}\left(\frac{\mathrm{2}}{\mathrm{5}}\right) \\ $$$${x}={log}\left(−\mathrm{1}\right)=\pi{i} \\ $$
