Question Number 114802 by aurpeyz last updated on 21/Sep/20
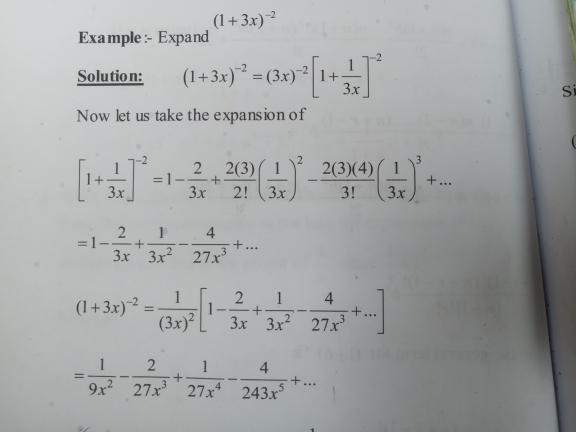
Answered by aurpeyz last updated on 21/Sep/20
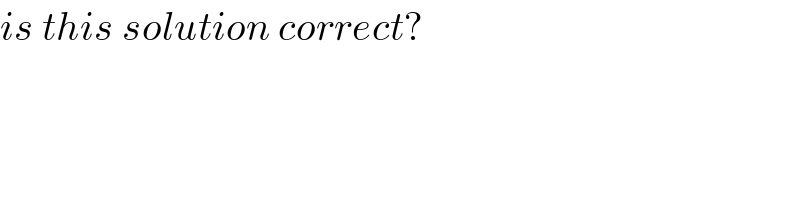
$${is}\:{this}\:{solution}\:{correct}? \\ $$
Commented by mr W last updated on 21/Sep/20

$${yes} \\ $$
Commented by aurpeyz last updated on 21/Sep/20
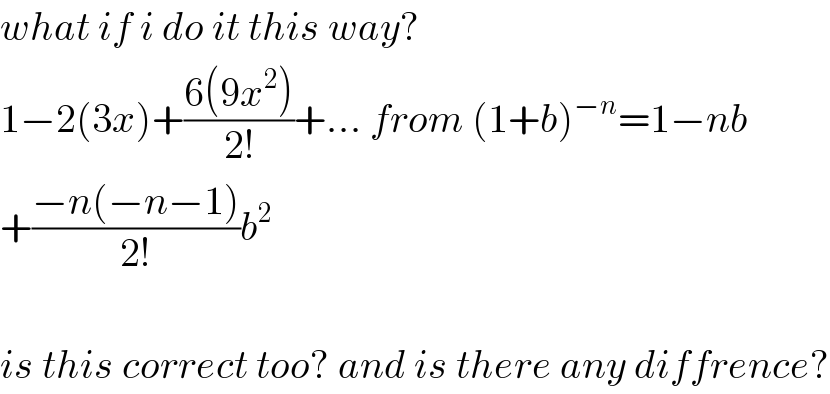
$${what}\:{if}\:{i}\:{do}\:{it}\:{this}\:{way}? \\ $$$$\mathrm{1}−\mathrm{2}\left(\mathrm{3}{x}\right)+\frac{\mathrm{6}\left(\mathrm{9}{x}^{\mathrm{2}} \right)}{\mathrm{2}!}+…\:{from}\:\left(\mathrm{1}+{b}\right)^{−{n}} =\mathrm{1}−{nb} \\ $$$$+\frac{−{n}\left(−{n}−\mathrm{1}\right)}{\mathrm{2}!}{b}^{\mathrm{2}} \\ $$$$ \\ $$$${is}\:{this}\:{correct}\:{too}?\:{and}\:{is}\:{there}\:{any}\:{diffrence}? \\ $$
Commented by mr W last updated on 21/Sep/20
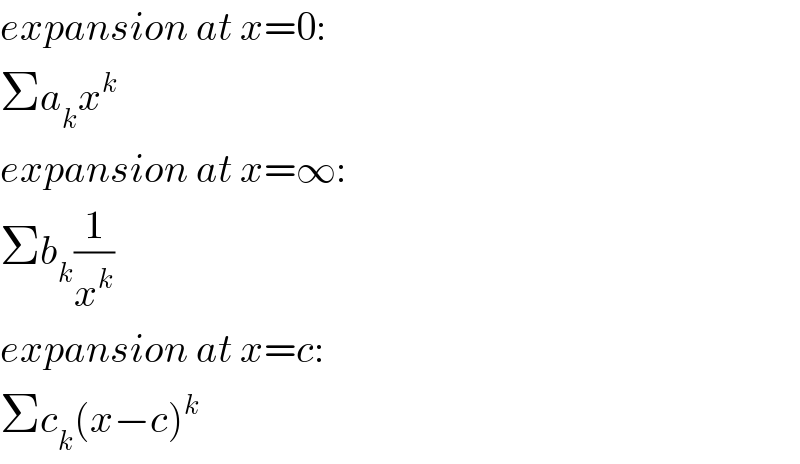
$${expansion}\:{at}\:{x}=\mathrm{0}: \\ $$$$\Sigma{a}_{{k}} {x}^{{k}} \\ $$$${expansion}\:{at}\:{x}=\infty: \\ $$$$\Sigma{b}_{{k}} \frac{\mathrm{1}}{{x}^{{k}} } \\ $$$${expansion}\:{at}\:{x}={c}: \\ $$$$\Sigma{c}_{{k}} \left({x}−{c}\right)^{{k}} \\ $$
Commented by aurpeyz last updated on 22/Sep/20
$${pls}\:{can}\:{you}\:{explain}\:{this}? \\ $$
Commented by mr W last updated on 22/Sep/20
$${how}\:{about}\:{read}\:{a}\:{mathematics}\:{book} \\ $$$${by}\:{yourself}? \\ $$
Commented by aurpeyz last updated on 22/Sep/20

$${okay}\:{sir} \\ $$
Commented by aurpeyz last updated on 23/Sep/20
![sir. with my study. i think the solution is wrong. from the solution. it is only valid if ∣(1/(3x))∣<1 which will yield x>(1/3) or x<((−1)/3) which implies the range of validity of the expansion. if i test the expansion by substituting a value in the region lf validity. x=1 (1+3(1))^(−2) ≠(1/(9(1)))−(2/(27(1)))+... but if expand it in this approach ⇒ (1+3x)^(−2) =1−6x+(((6)9x^2 )/(2!))... which is valid if the ∣3x∣<1 i.e. ∣x∣<(1/3) if x=0 [within the range of validity. ] (1+0)^(−2) =1−6(0)+...=1=1](https://www.tinkutara.com/question/Q115061.png)
$$ \\ $$$${sir}.\:{with}\:{my}\:{study}.\:{i}\:{think}\:{the}\:{solution}\:{is}\:{wrong}. \\ $$$${from}\:{the}\:{solution}.\:{it}\:{is}\:{only}\:{valid}\:{if}\: \\ $$$$\mid\frac{\mathrm{1}}{\mathrm{3}{x}}\mid<\mathrm{1}\:{which}\:{will}\:{yield}\:{x}>\frac{\mathrm{1}}{\mathrm{3}}\:{or}\:{x}<\frac{−\mathrm{1}}{\mathrm{3}}\: \\ $$$${which}\:{implies}\:{the}\:{range}\:{of}\:{validity}\:{of}\:{the}\: \\ $$$${expansion}.\: \\ $$$${if}\:{i}\:{test}\:{the}\:{expansion}\:{by}\:{substituting}\:{a} \\ $$$${value}\:{in}\:{the}\:{region}\:{lf}\:{validity}.\:{x}=\mathrm{1} \\ $$$$\left(\mathrm{1}+\mathrm{3}\left(\mathrm{1}\right)\right)^{−\mathrm{2}} \neq\frac{\mathrm{1}}{\mathrm{9}\left(\mathrm{1}\right)}−\frac{\mathrm{2}}{\mathrm{27}\left(\mathrm{1}\right)}+… \\ $$$${but}\:{if}\:{expand}\:{it}\:{in}\:{this}\:{approach}\:\Rightarrow \\ $$$$\left(\mathrm{1}+\mathrm{3}{x}\right)^{−\mathrm{2}} =\mathrm{1}−\mathrm{6}{x}+\frac{\left(\mathrm{6}\right)\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}!}…\:{which}\:{is}\:{valid} \\ $$$${if}\:{the}\:\mid\mathrm{3}{x}\mid<\mathrm{1}\:\:{i}.{e}.\:\mid{x}\mid<\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:{if}\:{x}=\mathrm{0}\:\left[{within}\right. \\ $$$$\left.{the}\:{range}\:{of}\:{validity}.\:\right] \\ $$$$\left(\mathrm{1}+\mathrm{0}\right)^{−\mathrm{2}} =\mathrm{1}−\mathrm{6}\left(\mathrm{0}\right)+…=\mathrm{1}=\mathrm{1} \\ $$
