Question Number 114860 by mathdave last updated on 21/Sep/20

Commented by Dwaipayan Shikari last updated on 21/Sep/20
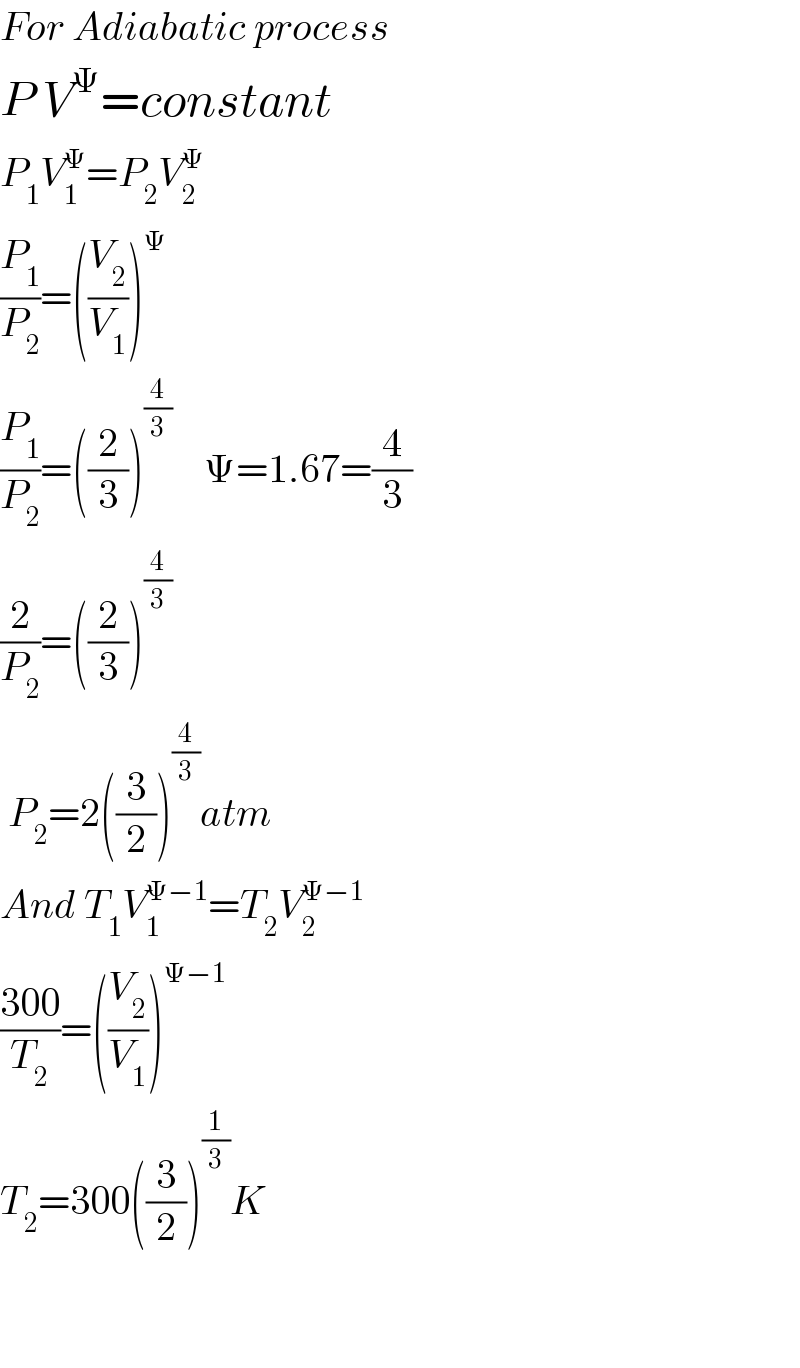
$${For}\:{Adiabatic}\:{process} \\ $$$${P}\:{V}^{\Psi} ={constant} \\ $$$${P}_{\mathrm{1}} {V}_{\mathrm{1}} ^{\Psi} ={P}_{\mathrm{2}} {V}_{\mathrm{2}} ^{\Psi} \\ $$$$\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }=\left(\frac{{V}_{\mathrm{2}} }{{V}_{\mathrm{1}} }\right)^{\Psi} \\ $$$$\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }=\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \:\:\:\:\Psi=\mathrm{1}.\mathrm{67}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\frac{\mathrm{2}}{{P}_{\mathrm{2}} }=\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \\ $$$$\:{P}_{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} {atm} \\ $$$${And}\:{T}_{\mathrm{1}} {V}_{\mathrm{1}} ^{\Psi−\mathrm{1}} ={T}_{\mathrm{2}} {V}_{\mathrm{2}} ^{\Psi−\mathrm{1}} \\ $$$$\frac{\mathrm{300}}{{T}_{\mathrm{2}} }=\left(\frac{{V}_{\mathrm{2}} }{{V}_{\mathrm{1}} }\right)^{\Psi−\mathrm{1}} \\ $$$${T}_{\mathrm{2}} =\mathrm{300}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {K} \\ $$$$ \\ $$$$ \\ $$
Commented by mathdave last updated on 21/Sep/20
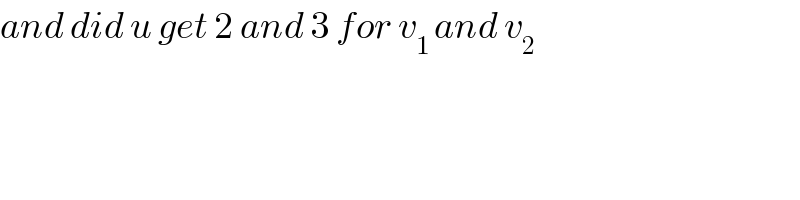
$${and}\:{did}\:{u}\:{get}\:\mathrm{2}\:{and}\:\mathrm{3}\:{for}\:{v}_{\mathrm{1}\:} {and}\:{v}_{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 21/Sep/20
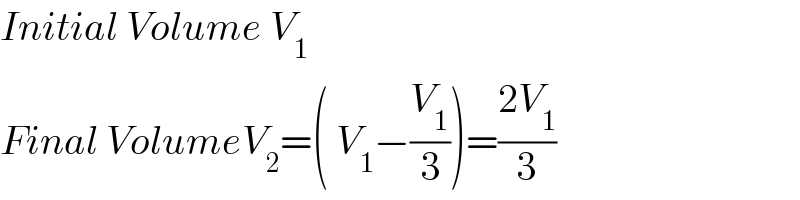
$${Initial}\:{Volume}\:{V}_{\mathrm{1}} \\ $$$${Final}\:{VolumeV}_{\mathrm{2}} =\left(\:{V}_{\mathrm{1}} −\frac{{V}_{\mathrm{1}} }{\mathrm{3}}\right)=\frac{\mathrm{2}{V}_{\mathrm{1}} }{\mathrm{3}} \\ $$
