Menu Close

Question-114945

Tinku Tara 0 Comments
Pin




Question Number 114945 by bemath last updated on 22/Sep/20
Answered by bobhans last updated on 22/Sep/20
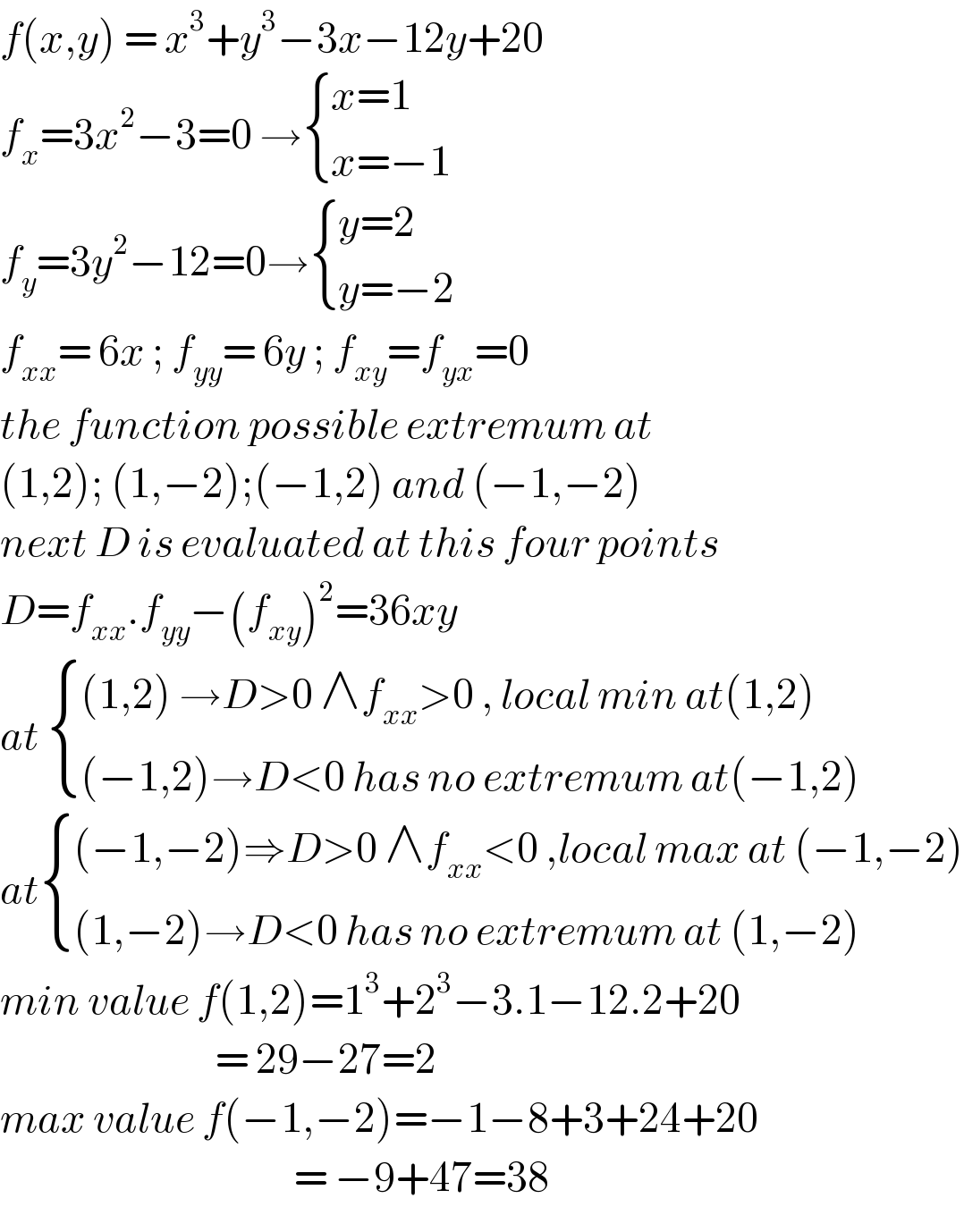
f(x,y) = x^3 +y^3 −3x−12y+20 f_x =3x^2 −3=0 → { ((x=1)),((x=−1)) :} f_y =3y^2 −12=0→ { ((y=2)),((y=−2)) :} f_(xx) = 6x ; f_(yy) = 6y ; f_(xy) =f_(yx) =0 the function possible extremum at (1,2); (1,−2);(−1,2) and (−1,−2) next D is evaluated at this four points D=f_(xx) .f_(yy) −(f_(xy) )^2 =36xy at { (((1,2) →D>0 ∧f_(xx) >0 , local min at(1,2))),(((−1,2)→D<0 has no extremum at(−1,2))) :} at { (((−1,−2)⇒D>0 ∧f_(xx) <0 ,local max at (−1,−2))),(((1,−2)→D<0 has no extremum at (1,−2))) :} min value f(1,2)=1^3 +2^3 −3.1−12.2+20 = 29−27=2 max value f(−1,−2)=−1−8+3+24+20 = −9+47=38
$${f}\left({x},{y}\right)\:=\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{12}{y}+\mathrm{20} \\ $$$${f}_{{x}} =\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}=\mathrm{0}\:\rightarrow\begin{cases}{{x}=\mathrm{1}}\\{{x}=−\mathrm{1}}\end{cases} \\ $$$${f}_{{y}} =\mathrm{3}{y}^{\mathrm{2}} −\mathrm{12}=\mathrm{0}\rightarrow\begin{cases}{{y}=\mathrm{2}}\\{{y}=−\mathrm{2}}\end{cases} \\ $$$${f}_{{xx}} =\:\mathrm{6}{x}\:;\:{f}_{{yy}} =\:\mathrm{6}{y}\:;\:{f}_{{xy}} ={f}_{{yx}} =\mathrm{0} \\ $$$${the}\:{function}\:{possible}\:{extremum}\:{at}\: \\ $$$$\left(\mathrm{1},\mathrm{2}\right);\:\left(\mathrm{1},−\mathrm{2}\right);\left(−\mathrm{1},\mathrm{2}\right)\:{and}\:\left(−\mathrm{1},−\mathrm{2}\right) \\ $$$${next}\:{D}\:{is}\:{evaluated}\:{at}\:{this}\:{four}\:{points} \\ $$$${D}={f}_{{xx}} .{f}_{{yy}} −\left({f}_{{xy}} \right)^{\mathrm{2}} =\mathrm{36}{xy} \\ $$$${at}\:\begin{cases}{\left(\mathrm{1},\mathrm{2}\right)\:\rightarrow{D}>\mathrm{0}\:\wedge{f}_{{xx}} >\mathrm{0}\:,\:{local}\:{min}\:{at}\left(\mathrm{1},\mathrm{2}\right)}\\{\left(−\mathrm{1},\mathrm{2}\right)\rightarrow{D}<\mathrm{0}\:{has}\:{no}\:{extremum}\:{at}\left(−\mathrm{1},\mathrm{2}\right)}\end{cases} \\ $$$${at\begin{cases}{\left(−\mathrm{1},−\mathrm{2}\right)\Rightarrow{D}>\mathrm{0}\:\wedge{f}_{{xx}} <\mathrm{0}\:,{local}\:{max}\:{at}\:\left(−\mathrm{1},−\mathrm{2}\right)}\\{\left(\mathrm{1},−\mathrm{2}\right)\rightarrow{D}<\mathrm{0}\:{has}\:{no}\:{extremum}\:{at}\:\left(\mathrm{1},−\mathrm{2}\right)}\end{cases}} \\ $$$${min}\:{value}\:{f}\left(\mathrm{1},\mathrm{2}\right)=\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} −\mathrm{3}.\mathrm{1}−\mathrm{12}.\mathrm{2}+\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{29}−\mathrm{27}=\mathrm{2} \\ $$$${max}\:{value}\:{f}\left(−\mathrm{1},−\mathrm{2}\right)=−\mathrm{1}−\mathrm{8}+\mathrm{3}+\mathrm{24}+\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{9}+\mathrm{47}=\mathrm{38} \\ $$
Commented by bemath last updated on 22/Sep/20
santuyy...sir. gave kudos
$${santuyy}…{sir}.\:{gave}\:{kudos} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *