Menu Close

Question-115056

Tinku Tara 0 Comments
Pin




Question Number 115056 by A8;15: last updated on 23/Sep/20
Answered by 1549442205PVT last updated on 23/Sep/20
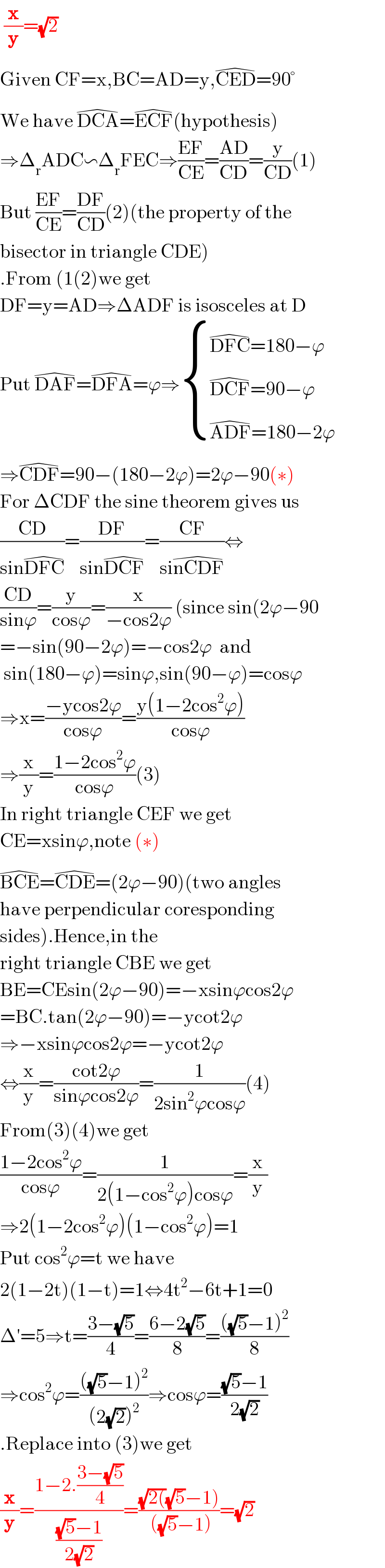
(x/y)=(√2) Given CF=x,BC=AD=y,CED^(�) =90° We have DCA^(�) =ECF^(�) (hypothesis) ⇒Δ_r ADC∽Δ_r FEC⇒((EF)/(CE))=((AD)/(CD))=(y/(CD))(1) But ((EF)/(CE))=((DF)/(CD))(2)(the property of the bisector in triangle CDE) .From (1(2)we get DF=y=AD⇒ΔADF is isosceles at D Put DAF^(�) =DFA^(�) =ϕ⇒ { ((DFC^(�) =180−ϕ)),((DCF^(�) =90−ϕ)),((ADF^(�) =180−2ϕ)) :} ⇒CDF^(�) =90−(180−2ϕ)=2ϕ−90(∗) For ΔCDF the sine theorem gives us ((CD)/(sinDFC^(�) ))=((DF)/(sinDCF^(�) ))=((CF)/(sinCDF^(�) ))⇔ ((CD)/(sinϕ))=(y/(cosϕ))=(x/(−cos2ϕ)) (since sin(2ϕ−90 =−sin(90−2ϕ)=−cos2ϕ and sin(180−ϕ)=sinϕ,sin(90−ϕ)=cosϕ ⇒x=((−ycos2ϕ)/(cosϕ))=((y(1−2cos^2 ϕ))/(cosϕ)) ⇒(x/y)=((1−2cos^2 ϕ)/(cosϕ))(3) In right triangle CEF we get CE=xsinϕ,note (∗) BCE^(�) =CDE^(�) =(2ϕ−90)(two angles have perpendicular coresponding sides).Hence,in the right triangle CBE we get BE=CEsin(2ϕ−90)=−xsinϕcos2ϕ =BC.tan(2ϕ−90)=−ycot2ϕ ⇒−xsinϕcos2ϕ=−ycot2ϕ ⇔(x/y)=((cot2ϕ)/(sinϕcos2ϕ))=(1/(2sin^2 ϕcosϕ))(4) From(3)(4)we get ((1−2cos^2 ϕ)/(cosϕ))=(1/(2(1−cos^2 ϕ)cosϕ))=(x/y) ⇒2(1−2cos^2 ϕ)(1−cos^2 ϕ)=1 Put cos^2 ϕ=t we have 2(1−2t)(1−t)=1⇔4t^2 −6t+1=0 Δ′=5⇒t=((3−(√5))/4)=((6−2(√5))/8)=((((√5)−1)^2 )/8) ⇒cos^2 ϕ=((((√5)−1)^2 )/((2(√2))^2 ))⇒cosϕ=(((√5)−1)/(2(√2))) .Replace into (3)we get (x/y)=((1−2.((3−(√5))/4))/(((√5)−1)/(2(√2))))=(((√(2())(√5)−1))/( ((√5)−1)))=(√2)
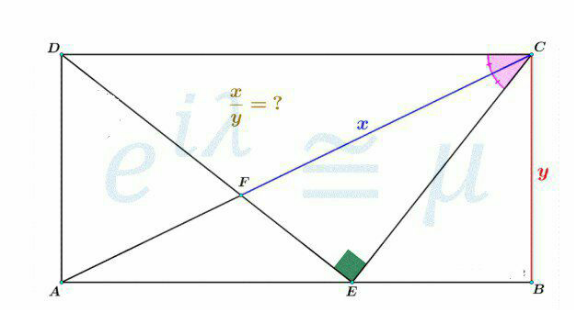
$$\:\frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{y}}}=\sqrt{\mathrm{2}} \\ $$$$\mathrm{Given}\:\mathrm{CF}=\mathrm{x},\mathrm{BC}=\mathrm{AD}=\mathrm{y},\widehat {\mathrm{CED}}=\mathrm{90}° \\ $$$$\mathrm{We}\:\mathrm{have}\:\widehat {\mathrm{DCA}}=\widehat {\mathrm{ECF}}\left(\mathrm{hypothesis}\right) \\ $$$$\Rightarrow\Delta_{\mathrm{r}} \mathrm{ADC}\backsim\Delta_{\mathrm{r}} \mathrm{FEC}\Rightarrow\frac{\mathrm{EF}}{\mathrm{CE}}=\frac{\mathrm{AD}}{\mathrm{CD}}=\frac{\mathrm{y}}{\mathrm{CD}}\left(\mathrm{1}\right) \\ $$$$\mathrm{But}\:\frac{\mathrm{EF}}{\mathrm{CE}}=\frac{\mathrm{DF}}{\mathrm{CD}}\left(\mathrm{2}\right)\left(\mathrm{the}\:\mathrm{property}\:\mathrm{of}\:\mathrm{the}\right. \\ $$$$\left.\mathrm{bisector}\:\mathrm{in}\:\mathrm{triangle}\:\mathrm{CDE}\right) \\ $$$$.\mathrm{From}\:\left(\mathrm{1}\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get}\right. \\ $$$$\mathrm{DF}=\mathrm{y}=\mathrm{AD}\Rightarrow\Delta\mathrm{ADF}\:\mathrm{is}\:\mathrm{isosceles}\:\mathrm{at}\:\mathrm{D} \\ $$$$\mathrm{Put}\:\widehat {\mathrm{DAF}}=\widehat {\mathrm{DFA}}=\varphi\Rightarrow\begin{cases}{\widehat {\mathrm{DFC}}=\mathrm{180}−\varphi}\\{\widehat {\mathrm{DCF}}=\mathrm{90}−\varphi}\\{\widehat {\mathrm{ADF}}=\mathrm{180}−\mathrm{2}\varphi}\end{cases} \\ $$$$\Rightarrow\widehat {\mathrm{CDF}}=\mathrm{90}−\left(\mathrm{180}−\mathrm{2}\varphi\right)=\mathrm{2}\varphi−\mathrm{90}\left(\ast\right) \\ $$$$\mathrm{For}\:\Delta\mathrm{CDF}\:\mathrm{the}\:\mathrm{sine}\:\mathrm{theorem}\:\mathrm{gives}\:\mathrm{us} \\ $$$$\frac{\mathrm{CD}}{\mathrm{sin}\widehat {\mathrm{DFC}}}=\frac{\mathrm{DF}}{\mathrm{sin}\widehat {\mathrm{DCF}}}=\frac{\mathrm{CF}}{\mathrm{si}\widehat {\mathrm{nCDF}}}\Leftrightarrow \\ $$$$\frac{\mathrm{CD}}{\mathrm{sin}\varphi}=\frac{\mathrm{y}}{\mathrm{cos}\varphi}=\frac{\mathrm{x}}{−\mathrm{cos2}\varphi}\:\left(\mathrm{since}\:\mathrm{sin}\left(\mathrm{2}\varphi−\mathrm{90}\right.\right. \\ $$$$=−\mathrm{sin}\left(\mathrm{90}−\mathrm{2}\varphi\right)=−\mathrm{cos2}\varphi\:\:\mathrm{and} \\ $$$$\:\mathrm{sin}\left(\mathrm{180}−\varphi\right)=\mathrm{sin}\varphi,\mathrm{sin}\left(\mathrm{90}−\varphi\right)=\mathrm{cos}\varphi \\ $$$$\Rightarrow\mathrm{x}=\frac{−\mathrm{ycos2}\varphi}{\mathrm{cos}\varphi}=\frac{\mathrm{y}\left(\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \varphi\right)}{\mathrm{cos}\varphi} \\ $$$$\Rightarrow\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \varphi}{\mathrm{cos}\varphi}\left(\mathrm{3}\right) \\ $$$$\mathrm{In}\:\mathrm{right}\:\mathrm{triangle}\:\mathrm{CEF}\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\mathrm{CE}=\mathrm{xsin}\varphi,\mathrm{note}\:\left(\ast\right) \\ $$$$\widehat {\mathrm{BCE}}=\widehat {\mathrm{CDE}}=\left(\mathrm{2}\varphi−\mathrm{90}\right)\left(\mathrm{two}\:\mathrm{angles}\:\right. \\ $$$$\mathrm{have}\:\mathrm{perpendicular}\:\mathrm{coresponding} \\ $$$$\left.\mathrm{sides}\right).\mathrm{Hence},\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{right}\:\mathrm{triangle}\:\mathrm{CBE}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{BE}=\mathrm{CEsin}\left(\mathrm{2}\varphi−\mathrm{90}\right)=−\mathrm{xsin}\varphi\mathrm{cos2}\varphi \\ $$$$=\mathrm{BC}.\mathrm{tan}\left(\mathrm{2}\varphi−\mathrm{90}\right)=−\mathrm{ycot2}\varphi \\ $$$$\Rightarrow−\mathrm{xsin}\varphi\mathrm{cos2}\varphi=−\mathrm{ycot2}\varphi \\ $$$$\Leftrightarrow\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{cot2}\varphi}{\mathrm{sin}\varphi\mathrm{cos2}\varphi}=\frac{\mathrm{1}}{\mathrm{2sin}^{\mathrm{2}} \varphi\mathrm{cos}\varphi}\left(\mathrm{4}\right) \\ $$$$\mathrm{From}\left(\mathrm{3}\right)\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \varphi}{\mathrm{cos}\varphi}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \varphi\right)\mathrm{cos}\varphi}=\frac{\mathrm{x}}{\mathrm{y}} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \varphi\right)\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \varphi\right)=\mathrm{1} \\ $$$$\mathrm{Put}\:\mathrm{cos}^{\mathrm{2}} \varphi=\mathrm{t}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{2}\left(\mathrm{1}−\mathrm{2t}\right)\left(\mathrm{1}−\mathrm{t}\right)=\mathrm{1}\Leftrightarrow\mathrm{4t}^{\mathrm{2}} −\mathrm{6t}+\mathrm{1}=\mathrm{0} \\ $$$$\Delta'=\mathrm{5}\Rightarrow\mathrm{t}=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}=\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{8}}=\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \varphi=\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\Rightarrow\mathrm{cos}\varphi=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{y}}}=\frac{\mathrm{1}−\mathrm{2}.\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}}{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}=\frac{\left.\sqrt{\mathrm{2}\left(\right.}\sqrt{\mathrm{5}}−\mathrm{1}\right)}{\:\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}=\sqrt{\mathrm{2}} \\ $$
Commented by A8;15: last updated on 23/Sep/20
how
Commented by A8;15: last updated on 23/Sep/20
please help me with the solution

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *