Question-115135

Question Number 115135 by Algoritm last updated on 23/Sep/20

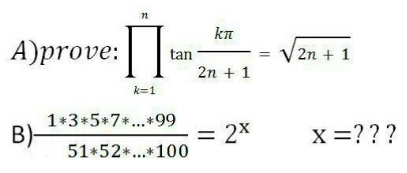
Commented by Dwaipayan Shikari last updated on 23/Sep/20

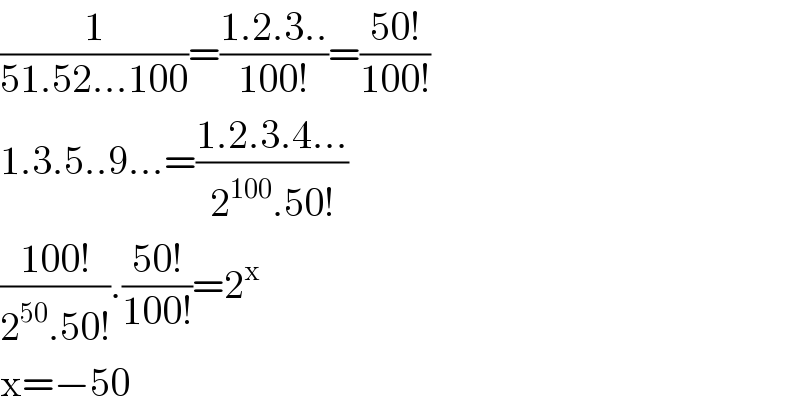
(1/(51.52...100))=((1.2.3..)/(100!))=((50!)/(100!)) 1.3.5..9...=((1.2.3.4...)/(2^(100) .50!)) ((100!)/(2^(50) .50!)).((50!)/(100!))=2^x x=−50

$$\frac{\mathrm{1}}{\mathrm{51}.\mathrm{52}…\mathrm{100}}=\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}..}{\mathrm{100}!}=\frac{\mathrm{50}!}{\mathrm{100}!} \\ $$$$\mathrm{1}.\mathrm{3}.\mathrm{5}..\mathrm{9}…=\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}…}{\mathrm{2}^{\mathrm{100}} .\mathrm{50}!} \\ $$$$\frac{\mathrm{100}!}{\mathrm{2}^{\mathrm{50}} .\mathrm{50}!}.\frac{\mathrm{50}!}{\mathrm{100}!}=\mathrm{2}^{\mathrm{x}} \\ $$$$\mathrm{x}=−\mathrm{50} \\ $$

Answered by Olaf last updated on 23/Sep/20

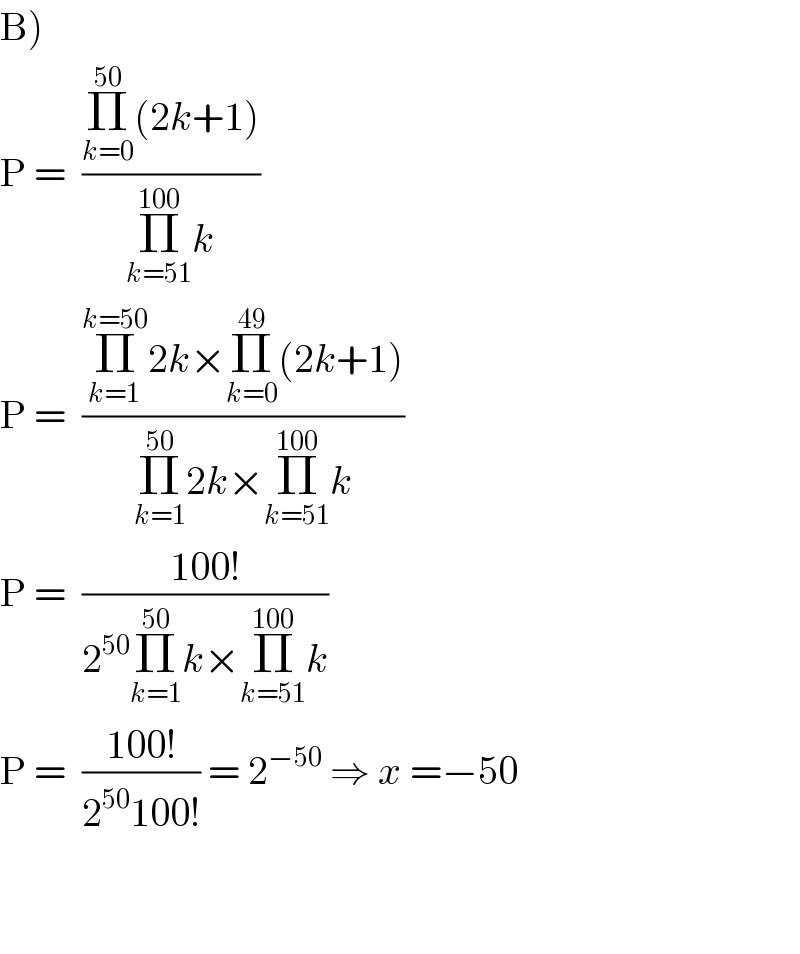
B) P = ((Π_(k=0) ^(50) (2k+1))/(Π_(k=51) ^(100) k)) P = ((Π_(k=1) ^(k=50) 2k×Π_(k=0) ^(49) (2k+1))/(Π_(k=1) ^(50) 2k×Π_(k=51) ^(100) k)) P = ((100!)/(2^(50) Π_(k=1) ^(50) k×Π_(k=51) ^(100) k)) P = ((100!)/(2^(50) 100!)) = 2^(−50) ⇒ x =−50

$$\left.\mathrm{B}\right) \\ $$$$\mathrm{P}\:=\:\:\frac{\underset{{k}=\mathrm{0}} {\overset{\mathrm{50}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right)}{\underset{{k}=\mathrm{51}} {\overset{\mathrm{100}} {\prod}}{k}} \\ $$$$\mathrm{P}\:=\:\:\frac{\underset{{k}=\mathrm{1}} {\overset{{k}=\mathrm{50}} {\prod}}\mathrm{2}{k}×\underset{{k}=\mathrm{0}} {\overset{\mathrm{49}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right)}{\underset{{k}=\mathrm{1}} {\overset{\mathrm{50}} {\prod}}\mathrm{2}{k}×\underset{{k}=\mathrm{51}} {\overset{\mathrm{100}} {\prod}}{k}} \\ $$$$\mathrm{P}\:=\:\:\frac{\mathrm{100}!}{\mathrm{2}^{\mathrm{50}} \underset{{k}=\mathrm{1}} {\overset{\mathrm{50}} {\prod}}{k}×\underset{{k}=\mathrm{51}} {\overset{\mathrm{100}} {\prod}}{k}} \\ $$$$\mathrm{P}\:=\:\:\frac{\mathrm{100}!}{\mathrm{2}^{\mathrm{50}} \mathrm{100}!}\:=\:\mathrm{2}^{−\mathrm{50}} \:\Rightarrow\:{x}\:=−\mathrm{50} \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply