Menu Close

Question-115166

Tinku Tara 0 Comments
Pin




Question Number 115166 by I want to learn more last updated on 24/Sep/20
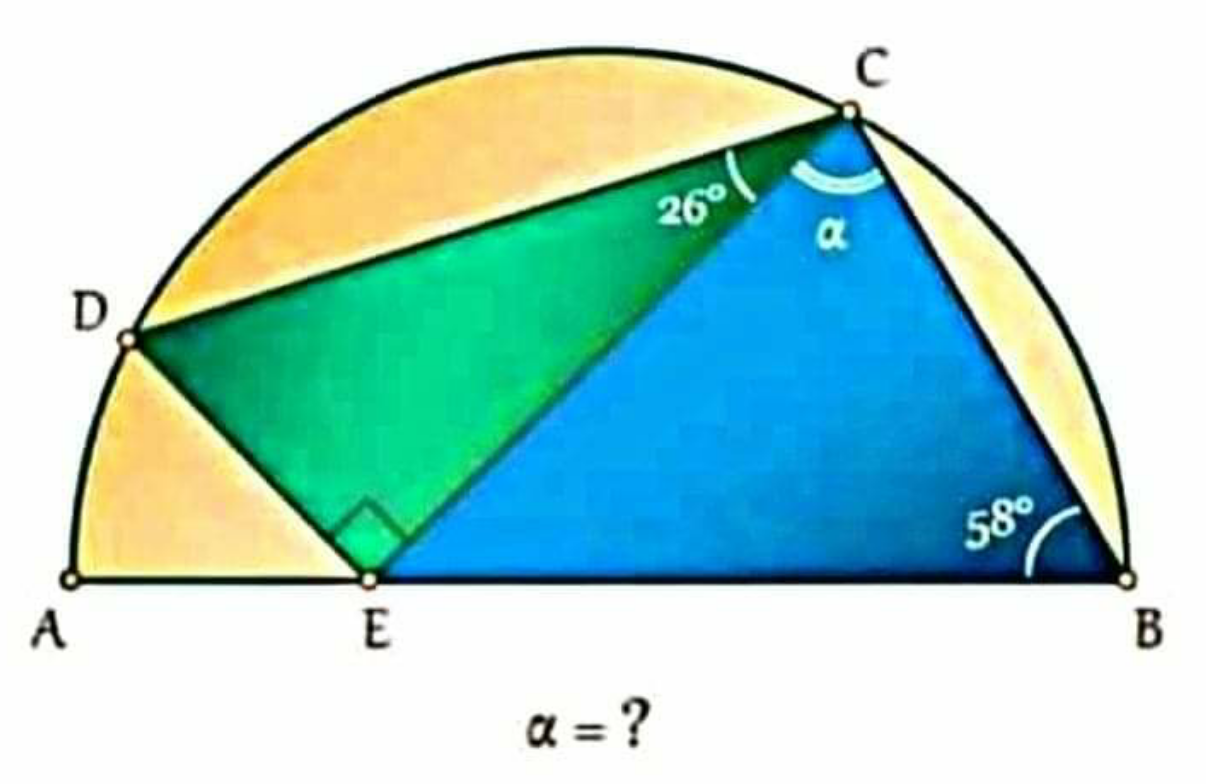
Answered by 1549442205PVT last updated on 24/Sep/20
77°
$$\mathrm{77}° \\ $$
Commented by I want to learn more last updated on 24/Sep/20
please workings sir
$$\mathrm{please}\:\mathrm{workings}\:\mathrm{sir} \\ $$
Answered by 1549442205PVT last updated on 24/Sep/20
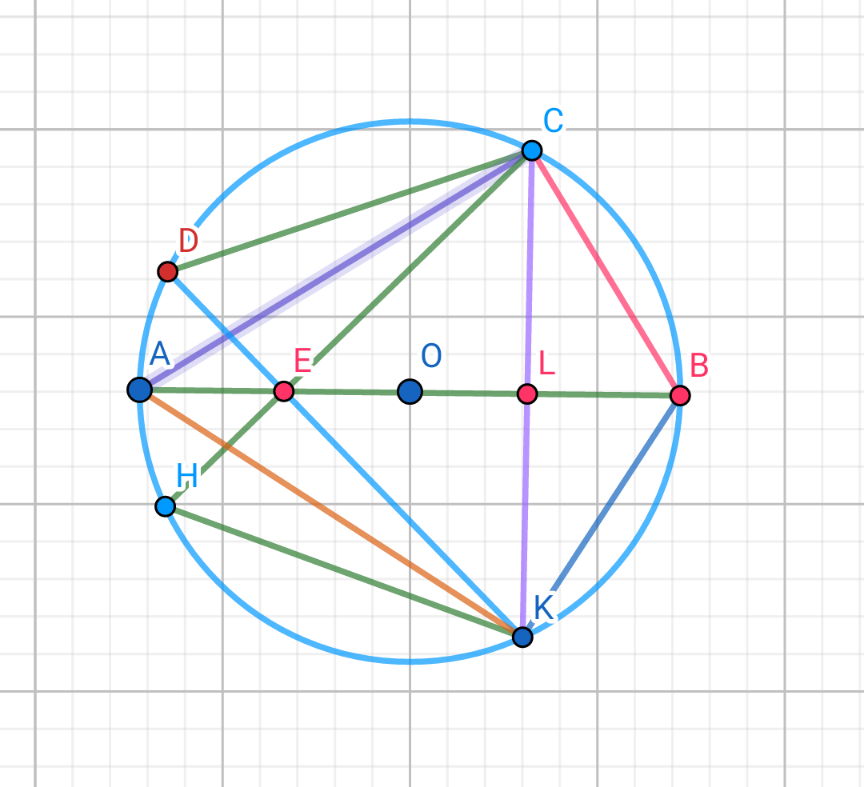
Commented by 1549442205PVT last updated on 24/Sep/20
Draw the circum circle (O)of ΔABC and denote K=(O)∩(DE),L=AB∩CK H=(O)∩(CE) From the hypothesis ΔCDE is right at E and DCE^(�) =26°⇒CDK^(�) =64°, ΔACB is right at C and ABC^(�) =58° ⇒BAC^(�) =32°=(1/2)CDK^(�) ⇒CBK^(⌢) =2BC^(⌢) ⇒BC^(⌢) =BK^(⌢) ⇒AB⊥CK at L(the property of the diameter of a circle)and BC=BK,LC=LK It follows that the triangles BCK and ECK are isosceles at B and E.Hence, AED^(�) =AEH^(�) =BEC^(�) =BEK^(�) =ϕ ⇒AD^(⌢) =AH^(⌢) ⇒CA is the bisector of the angle DCE^(�) =26°⇒ACD^(�) =ACH^(�) =13° ⇒α=ACB^(�) −ACH^(�) =90°−13°=77° Answer α=77°
$$\mathrm{Draw}\:\mathrm{the}\:\mathrm{circum}\:\mathrm{circle}\:\left(\mathrm{O}\right)\mathrm{of}\:\Delta\mathrm{ABC} \\ $$$$\mathrm{and}\:\mathrm{denote}\:\mathrm{K}=\left(\mathrm{O}\right)\cap\left(\mathrm{DE}\right),\mathrm{L}=\mathrm{AB}\cap\mathrm{CK} \\ $$$$\mathrm{H}=\left(\mathrm{O}\right)\cap\left(\mathrm{CE}\right) \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\Delta\mathrm{CDE}\:\mathrm{is}\:\mathrm{right} \\ $$$$\mathrm{at}\:\mathrm{E}\:\mathrm{and}\:\widehat {\mathrm{DCE}}=\mathrm{26}°\Rightarrow\widehat {\mathrm{CDK}}=\mathrm{64}°, \\ $$$$\Delta\mathrm{ACB}\:\mathrm{is}\:\mathrm{right}\:\mathrm{at}\:\mathrm{C}\:\mathrm{and}\:\widehat {\mathrm{ABC}}=\mathrm{58}° \\ $$$$\Rightarrow\widehat {\mathrm{BAC}}=\mathrm{32}°=\frac{\mathrm{1}}{\mathrm{2}}\widehat {\mathrm{CDK}}\Rightarrow\overset{\frown} {\mathrm{CBK}}=\mathrm{2}\overset{\frown} {\mathrm{BC}} \\ $$$$\Rightarrow\overset{\frown} {\mathrm{BC}}=\overset{\frown} {\mathrm{BK}}\:\Rightarrow\mathrm{AB}\bot\mathrm{CK}\:\mathrm{at}\:\mathrm{L}\left(\mathrm{the}\:\mathrm{property}\right. \\ $$$$\left.\mathrm{of}\:\mathrm{the}\:\mathrm{diameter}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\right)\mathrm{and}\:\mathrm{BC}=\mathrm{BK},\mathrm{LC}=\mathrm{LK} \\ $$$$\mathrm{It}\:\mathrm{follows}\:\mathrm{that}\:\mathrm{the}\:\mathrm{triangles}\:\mathrm{BCK}\:\mathrm{and} \\ $$$$\mathrm{ECK}\:\mathrm{are}\:\mathrm{isosceles}\:\mathrm{at}\:\mathrm{B}\:\mathrm{and}\:\mathrm{E}.\mathrm{Hence}, \\ $$$$\widehat {\mathrm{AED}}=\widehat {\mathrm{AEH}}=\widehat {\mathrm{BEC}}=\widehat {\mathrm{BEK}}=\varphi \\ $$$$\Rightarrow\overset{\frown} {\mathrm{AD}}=\overset{\frown} {\mathrm{AH}}\Rightarrow\mathrm{CA}\:\mathrm{is}\:\mathrm{the}\:\mathrm{bisector}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{angle}\:\:\widehat {\mathrm{DCE}}=\mathrm{26}°\Rightarrow\widehat {\mathrm{ACD}}=\widehat {\mathrm{ACH}}=\mathrm{13}° \\ $$$$\Rightarrow\alpha=\widehat {\mathrm{ACB}}−\widehat {\mathrm{ACH}}=\mathrm{90}°−\mathrm{13}°=\mathrm{77}° \\ $$$$\mathrm{Answer}\:\alpha=\mathrm{77}° \\ $$
Commented by I want to learn more last updated on 24/Sep/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *