Question Number 115333 by zakirullah last updated on 25/Sep/20

Commented by zakirullah last updated on 25/Sep/20

$${solve}\:{only}\:{Q}\left(\mathrm{5},\mathrm{6}\right) \\ $$
Commented by bemath last updated on 25/Sep/20
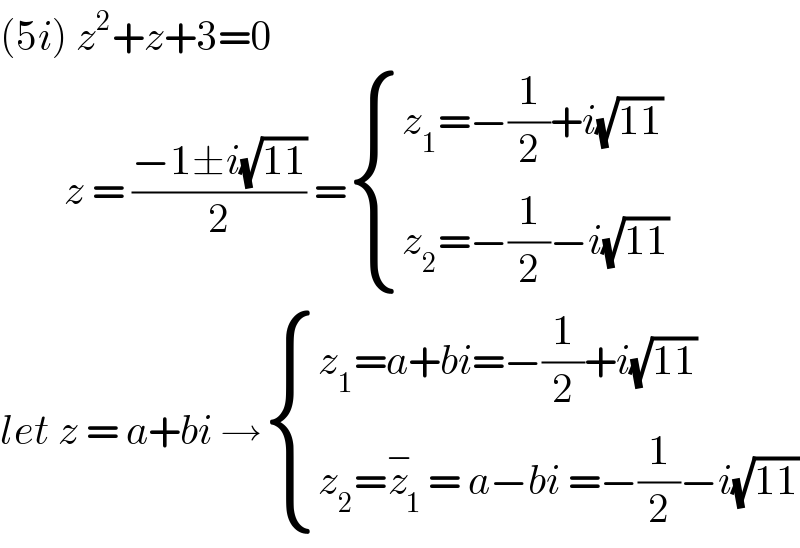
$$\left(\mathrm{5}{i}\right)\:{z}^{\mathrm{2}} +{z}+\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{z}\:=\:\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\:=\begin{cases}{{z}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}+{i}\sqrt{\mathrm{11}}}\\{{z}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}−{i}\sqrt{\mathrm{11}}}\end{cases} \\ $$$${let}\:{z}\:=\:{a}+{bi}\:\rightarrow\begin{cases}{{z}_{\mathrm{1}} ={a}+{bi}=−\frac{\mathrm{1}}{\mathrm{2}}+{i}\sqrt{\mathrm{11}}}\\{{z}_{\mathrm{2}} =\overset{−} {{z}}_{\mathrm{1}} =\:{a}−{bi}\:=−\frac{\mathrm{1}}{\mathrm{2}}−{i}\sqrt{\mathrm{11}}}\end{cases} \\ $$
Commented by zakirullah last updated on 25/Sep/20
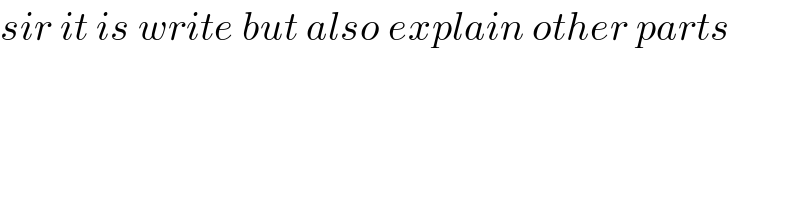
$${sir}\:{it}\:{is}\:{write}\:{but}\:{also}\:{explain}\:{other}\:{parts} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20
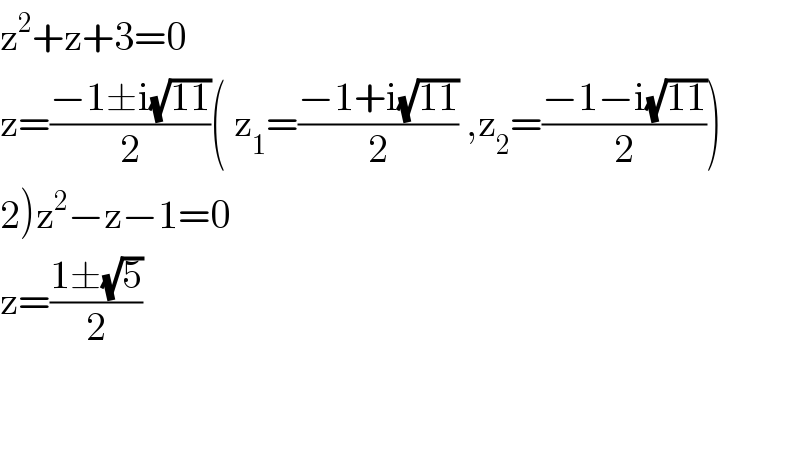
$$\mathrm{z}^{\mathrm{2}} +\mathrm{z}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{z}=\frac{−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\left(\:\mathrm{z}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\:,\mathrm{z}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{z}^{\mathrm{2}} −\mathrm{z}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{z}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
