Question Number 115387 by bemath last updated on 25/Sep/20

Commented by bemath last updated on 25/Sep/20
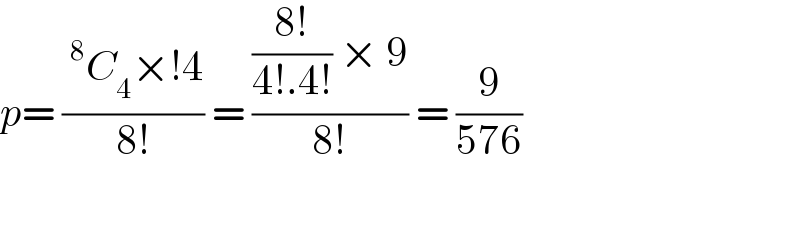
$${p}=\:\frac{\:^{\mathrm{8}} {C}_{\mathrm{4}} ×!\mathrm{4}}{\mathrm{8}!}\:=\:\frac{\frac{\mathrm{8}!}{\mathrm{4}!.\mathrm{4}!}\:×\:\mathrm{9}}{\mathrm{8}!}\:=\:\frac{\mathrm{9}}{\mathrm{576}} \\ $$$$ \\ $$
Commented by bemath last updated on 25/Sep/20
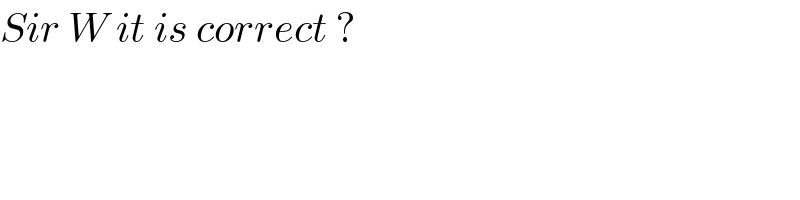
$${Sir}\:{W}\:{it}\:{is}\:{correct}\:? \\ $$
Commented by mr W last updated on 25/Sep/20
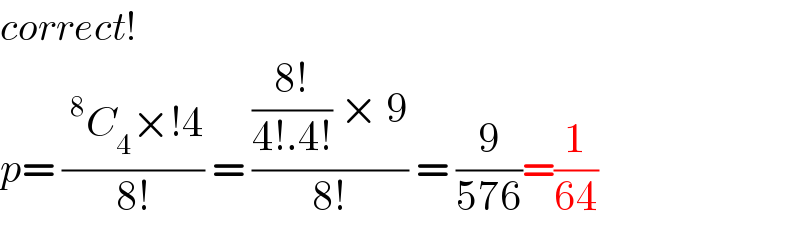
$${correct}! \\ $$$${p}=\:\frac{\:^{\mathrm{8}} {C}_{\mathrm{4}} ×!\mathrm{4}}{\mathrm{8}!}\:=\:\frac{\frac{\mathrm{8}!}{\mathrm{4}!.\mathrm{4}!}\:×\:\mathrm{9}}{\mathrm{8}!}\:=\:\frac{\mathrm{9}}{\mathrm{576}}=\frac{\mathrm{1}}{\mathrm{64}} \\ $$
Commented by indalecioneves last updated on 30/Sep/20
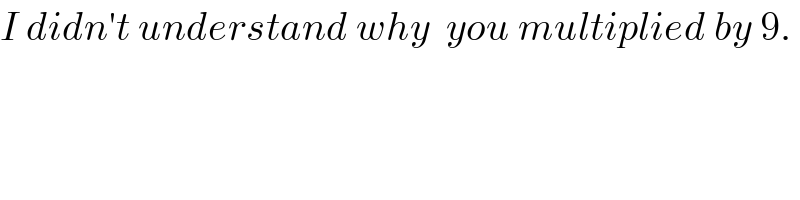
$${I}\:{didn}'{t}\:{understand}\:{why}\:\:{you}\:{multiplied}\:{by}\:\mathrm{9}. \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 30/Sep/20

$$!\mathrm{4}=\mathrm{9} \\ $$
Commented by indalecioneves last updated on 01/Oct/20

$${Oh},\:{yes},\:{chaotic}\:{permutation}.\: \\ $$$${I}\:{haven}'{t}\:{solved}\:{exercises}\:{with}\:{this}\:{theme} \\ $$$${for}\:{a}\:{long}\:{tine}.\:{Thanks},\:{Sir}. \\ $$
