Menu Close

Question-115597

Tinku Tara 0 Comments
Pin




Question Number 115597 by aurpeyz last updated on 26/Sep/20
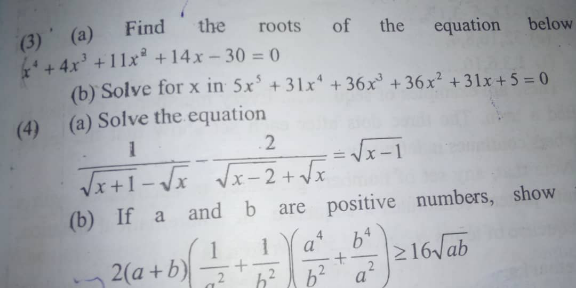
Answered by 1549442205PVT last updated on 27/Sep/20
4a)Solve the equation: (1/( (√(x+1))−(√x)))−(2/( (√(x−2))+(√x)))=(√(x−1)) ⇔(((√(x+1))+(√x))/1)−((2((√x)−(√(x−2))))/2)=(√(x−1)) ⇔(√(x+1))+(√x)−(√x)+(√(x−2))=(√(x−1)) ⇔(√(x+1))+(√(x−2))=(√(x−1)) (1) We need the condition:x≥2.Then (1)⇔x+1+x−2+2(√((x+1)(x−2)))=x−1 ⇔−x=2(√(x^2 −x−2)) This equation has no roots since for ∀x≥2 ⇒LHS<0,RHS≥0 b)Prove that ∀a,b>0 2(a+b)((1/a^2 )+(1/b^2 ))((a^4 /b^2 )+(b^4 /a^2 ))≥16(√(ab)) (∗) We have (1/a^2 )+(1/b^2 )=((1/a)−(1/b))^2 +(2/(ab))≥(2/(ab))(1) (a^4 /b^2 )+(b^4 /a^2 )=((a^2 /b)−(b^2 /a))^2 +2ab(2) a+b=((√(a−))(√b))^2 +2(√(ab))≥2(√(ab)) (3) Multiplying three above inequalities we get 2(a+b)((1/a^2 )+(1/b^2 ))((a^4 /b^2 )+(b^4 /a^2 )) ≥2.(2/(ab)).2ab.2(√(ab))=16(√(ab)) .Hence,the inequality (∗)is proved
$$\left.\mathrm{4a}\right)\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\mathrm{1}}−\sqrt{\mathrm{x}}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{x}−\mathrm{2}}+\sqrt{\mathrm{x}}}=\sqrt{\mathrm{x}−\mathrm{1}} \\ $$$$\Leftrightarrow\frac{\sqrt{\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{x}}}{\mathrm{1}}−\frac{\mathrm{2}\left(\sqrt{\mathrm{x}}−\sqrt{\mathrm{x}−\mathrm{2}}\right)}{\mathrm{2}}=\sqrt{\mathrm{x}−\mathrm{1}} \\ $$$$\Leftrightarrow\sqrt{\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{x}}−\sqrt{\mathrm{x}}+\sqrt{\mathrm{x}−\mathrm{2}}=\sqrt{\mathrm{x}−\mathrm{1}} \\ $$$$\Leftrightarrow\sqrt{\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{x}−\mathrm{2}}=\sqrt{\mathrm{x}−\mathrm{1}}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{the}\:\mathrm{condition}:\mathrm{x}\geqslant\mathrm{2}.\mathrm{Then} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{x}+\mathrm{1}+\mathrm{x}−\mathrm{2}+\mathrm{2}\sqrt{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)}=\mathrm{x}−\mathrm{1} \\ $$$$\Leftrightarrow−\mathrm{x}=\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}} \\ $$$$\mathrm{This}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots}\:\mathrm{since} \\ $$$$\mathrm{for}\:\forall\mathrm{x}\geqslant\mathrm{2}\:\Rightarrow\mathrm{LHS}<\mathrm{0},\mathrm{RHS}\geqslant\mathrm{0} \\ $$$$\left.\mathrm{b}\right)\mathrm{Prove}\:\mathrm{that}\:\forall\mathrm{a},\mathrm{b}>\mathrm{0} \\ $$$$\mathrm{2}\left(\mathrm{a}+\mathrm{b}\right)\left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{2}} }\right)\left(\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{b}^{\mathrm{2}} }+\frac{\mathrm{b}^{\mathrm{4}} }{\mathrm{a}^{\mathrm{2}} }\right)\geqslant\mathrm{16}\sqrt{\mathrm{ab}}\:\left(\ast\right) \\ $$$$\mathrm{We}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{2}} }=\left(\frac{\mathrm{1}}{\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{b}}\right)^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{ab}}\geqslant\frac{\mathrm{2}}{\mathrm{ab}}\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{b}^{\mathrm{2}} }+\frac{\mathrm{b}^{\mathrm{4}} }{\mathrm{a}^{\mathrm{2}} }=\left(\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{b}}−\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{a}}\right)^{\mathrm{2}} +\mathrm{2ab}\left(\mathrm{2}\right) \\ $$$$\mathrm{a}+\mathrm{b}=\left(\sqrt{\mathrm{a}−}\sqrt{\mathrm{b}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{ab}}\geqslant\mathrm{2}\sqrt{\mathrm{ab}}\:\:\left(\mathrm{3}\right) \\ $$$$\mathrm{Multiplying}\:\mathrm{three}\:\mathrm{above}\:\mathrm{inequalities} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{2}\left(\mathrm{a}+\mathrm{b}\right)\left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{2}} }\right)\left(\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{b}^{\mathrm{2}} }+\frac{\mathrm{b}^{\mathrm{4}} }{\mathrm{a}^{\mathrm{2}} }\right) \\ $$$$\geqslant\mathrm{2}.\frac{\mathrm{2}}{\mathrm{ab}}.\mathrm{2ab}.\mathrm{2}\sqrt{\mathrm{ab}}=\mathrm{16}\sqrt{\mathrm{ab}}\:.\mathrm{Hence},\mathrm{the} \\ $$$$\mathrm{inequality}\:\left(\ast\right)\mathrm{is}\:\mathrm{proved} \\ $$
Answered by TANMAY PANACEA last updated on 27/Sep/20
x^4 +4x^3 +11x^2 +14x−30 81−4×27+99−42−30 180−108−72=0→so (x+3) is factor x^4 +4x^3 +11x^2 +14x−30 =x^4 +3x^3 +x^3 +3x^2 +8x^2 +24x−10x−30 =x^3 (x+3) +x^2 (x+3) +8x (x+3) −10(x+3) =(x+3)(x^3 +x^2 +8x−10) =(x+3)(x^3 +x^2 +8x−10) so one root is x=−3 ★x^3 +x^2 +8x−10 =x^3 −x^2 +2x^2 −2x+10x−10 =x^2 (x−1) +2x (x−1)+10 (x−1) =(x−1)(x^2 +2x+10) another root x=1 x^2 +2x+10=0 x=((−2±(√(4−4×1×10)))/(2×1))=((−2±6i)/2)=−1±3i so roots are (−3,1,−1±3i)
$${x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{11}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{30} \\ $$$$\mathrm{81}−\mathrm{4}×\mathrm{27}+\mathrm{99}−\mathrm{42}−\mathrm{30} \\ $$$$\mathrm{180}−\mathrm{108}−\mathrm{72}=\mathrm{0}\rightarrow{so}\:\left({x}+\mathrm{3}\right)\:{is}\:{factor} \\ $$$${x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{11}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{30} \\ $$$$={x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{3}} +{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{8}{x}^{\mathrm{2}} +\mathrm{24}{x}−\mathrm{10}{x}−\mathrm{30} \\ $$$$={x}^{\mathrm{3}} \left({x}+\mathrm{3}\right)\:\:+{x}^{\mathrm{2}} \:\left({x}+\mathrm{3}\right)\:\:+\mathrm{8}{x}\:\left({x}+\mathrm{3}\right)\:\:\:−\mathrm{10}\left({x}+\mathrm{3}\right) \\ $$$$=\left({x}+\mathrm{3}\right)\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{10}\right) \\ $$$$=\left({x}+\mathrm{3}\right)\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{10}\right) \\ $$$${so}\:{one}\:{root}\:{is}\:{x}=−\mathrm{3} \\ $$$$\bigstar{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{10} \\ $$$$={x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{10}{x}−\mathrm{10} \\ $$$$={x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)\:+\mathrm{2}{x}\:\left({x}−\mathrm{1}\right)+\mathrm{10}\:\:\left({x}−\mathrm{1}\right) \\ $$$$=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}\right) \\ $$$${another}\:{root}\:{x}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}×\mathrm{1}×\mathrm{10}}}{\mathrm{2}×\mathrm{1}}=\frac{−\mathrm{2}\pm\mathrm{6}{i}}{\mathrm{2}}=−\mathrm{1}\pm\mathrm{3}{i} \\ $$$${so}\:{roots}\:{are}\:\left(−\mathrm{3},\mathrm{1},−\mathrm{1}\pm\mathrm{3}{i}\right) \\ $$$$ \\ $$
Answered by aurpeyz last updated on 26/Sep/20
4a
$$\mathrm{4}{a} \\ $$
Answered by TANMAY PANACEA last updated on 27/Sep/20
5x^5 +31x^4 +36x^3 +36x^2 +31x+5=0 5x^5 +5x^4 +26x^4 +26x^3 +10x^3 +10x^2 +26x^2 +26x+5x+5=0 5x^4 (x+1) +26x^3 (x+1) +10x^2 (x+1) +26x (x+1)+5 (x+1)=0 (x+1)(5x^4 +26x^3 +10x^2 +26x+5)=0 x=−1 is one root ★★now 5x^4 +26x^3 +10x^2 +26x+5=0→devide by x^2 5x^2 +(5/x^2 )+26x+((26)/x)+10=0 5{(x+(1/x))^2 −2}+26(x+(1/x))+10=0 5(x+(1/x))^2 +26(x+(1/x))=0 (x+(1/x))(5x+(5/x)+26)=0 (x+(1/x))=0→x^2 +1=0 x=±i (5x+(5/x)+26) 5x^2 +5+26x=0 5x^2 +25x+x+5=0 5x(x+5)+1(x+5)=0 (x+5)(5x+1)=0→x=−5,((−1)/5) so x=−1,−5,((−1)/5),±i
$$\mathrm{5}{x}^{\mathrm{5}} +\mathrm{31}{x}^{\mathrm{4}} +\mathrm{36}{x}^{\mathrm{3}} +\mathrm{36}{x}^{\mathrm{2}} +\mathrm{31}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{5}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} +\mathrm{26}{x}^{\mathrm{4}} +\mathrm{26}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{2}} +\mathrm{26}{x}^{\mathrm{2}} +\mathrm{26}{x}+\mathrm{5}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{5}{x}^{\mathrm{4}} \left({x}+\mathrm{1}\right)\:\:+\mathrm{26}{x}^{\mathrm{3}} \left({x}+\mathrm{1}\right)\:+\mathrm{10}{x}^{\mathrm{2}} \:\left({x}+\mathrm{1}\right)\:+\mathrm{26}{x}\:\left({x}+\mathrm{1}\right)+\mathrm{5}\:\:\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left(\mathrm{5}{x}^{\mathrm{4}} +\mathrm{26}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{2}} +\mathrm{26}{x}+\mathrm{5}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{1}\:\:{is}\:{one}\:{root} \\ $$$$\bigstar\bigstar{now} \\ $$$$\mathrm{5}{x}^{\mathrm{4}} +\mathrm{26}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{2}} +\mathrm{26}{x}+\mathrm{5}=\mathrm{0}\rightarrow{devide}\:{by}\:{x}^{\mathrm{2}} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\frac{\mathrm{5}}{{x}^{\mathrm{2}} }+\mathrm{26}{x}+\frac{\mathrm{26}}{{x}}+\mathrm{10}=\mathrm{0} \\ $$$$\mathrm{5}\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}\right\}+\mathrm{26}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{10}=\mathrm{0} \\ $$$$\mathrm{5}\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{26}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{5}{x}+\frac{\mathrm{5}}{{x}}+\mathrm{26}\right)=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{0}\rightarrow{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:\:{x}=\pm{i} \\ $$$$\left(\mathrm{5}{x}+\frac{\mathrm{5}}{{x}}+\mathrm{26}\right) \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{5}+\mathrm{26}{x}=\mathrm{0} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{25}{x}+{x}+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{5}{x}\left({x}+\mathrm{5}\right)+\mathrm{1}\left({x}+\mathrm{5}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{5}\right)\left(\mathrm{5}{x}+\mathrm{1}\right)=\mathrm{0}\rightarrow{x}=−\mathrm{5},\frac{−\mathrm{1}}{\mathrm{5}} \\ $$$${so}\:{x}=−\mathrm{1},−\mathrm{5},\frac{−\mathrm{1}}{\mathrm{5}},\pm{i} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *