Question Number 115632 by m173 last updated on 27/Sep/20

Commented by m173 last updated on 27/Sep/20
find general solution
Commented by MJS_new last updated on 27/Sep/20

$${y}={c}\mathrm{sin}\:{x}\:\mathrm{is}\:\mathrm{already}\:\mathrm{the}\:\mathrm{solution}?! \\ $$
Commented by mohammad17 last updated on 27/Sep/20
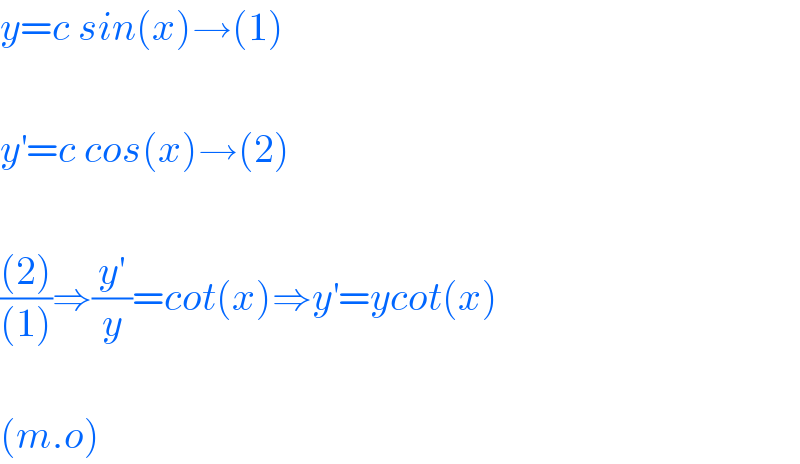
$${y}={c}\:{sin}\left({x}\right)\rightarrow\left(\mathrm{1}\right) \\ $$$$ \\ $$$${y}^{'} ={c}\:{cos}\left({x}\right)\rightarrow\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\frac{\left(\mathrm{2}\right)}{\left(\mathrm{1}\right)}\Rightarrow\frac{{y}^{'} }{{y}}={cot}\left({x}\right)\Rightarrow{y}^{'} ={ycot}\left({x}\right) \\ $$$$ \\ $$$$\left({m}.{o}\right) \\ $$
Commented by MJS_new last updated on 27/Sep/20
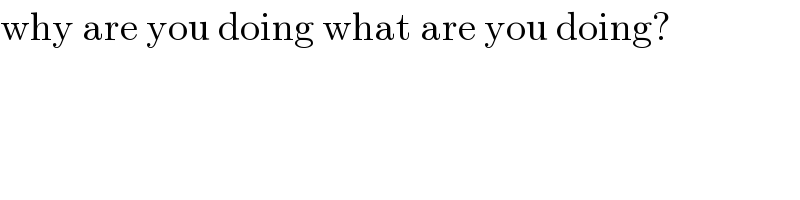
$$\mathrm{why}\:\mathrm{are}\:\mathrm{you}\:\mathrm{doing}\:\mathrm{what}\:\mathrm{are}\:\mathrm{you}\:\mathrm{doing}? \\ $$
Commented by Dwaipayan Shikari last updated on 27/Sep/20

$$\mathrm{sinx}=\frac{\mathrm{y}}{\mathrm{c}} \\ $$$$\mathrm{x}=\mathrm{k}\pi\pm\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{y}}{\mathrm{c}}\right) \\ $$
Commented by mathmax by abdo last updated on 27/Sep/20
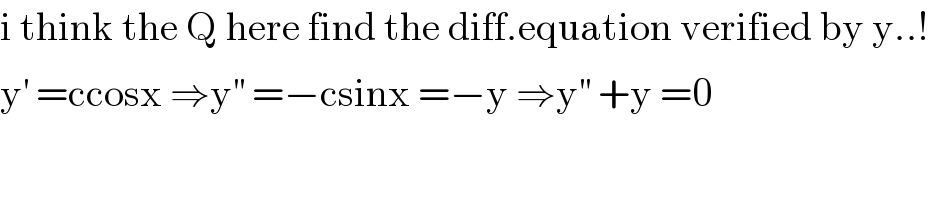
$$\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{Q}\:\mathrm{here}\:\mathrm{find}\:\mathrm{the}\:\mathrm{diff}.\mathrm{equation}\:\mathrm{verified}\:\mathrm{by}\:\mathrm{y}..! \\ $$$$\mathrm{y}^{'} \:=\mathrm{ccosx}\:\Rightarrow\mathrm{y}^{''} \:=−\mathrm{csinx}\:=−\mathrm{y}\:\Rightarrow\mathrm{y}^{''} \:+\mathrm{y}\:=\mathrm{0} \\ $$
Answered by PRITHWISH SEN 2 last updated on 27/Sep/20
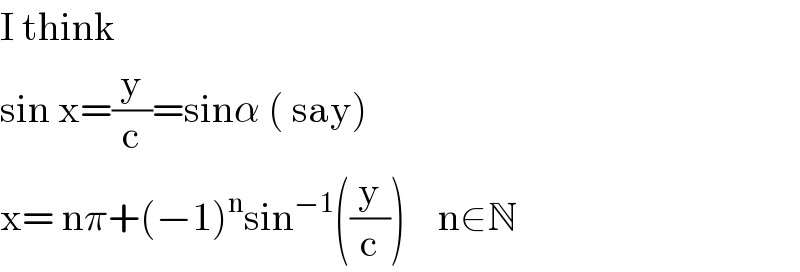
$$\mathrm{I}\:\mathrm{think} \\ $$$$\mathrm{sin}\:\mathrm{x}=\frac{\mathrm{y}}{\mathrm{c}}=\mathrm{sin}\alpha\:\left(\:\mathrm{say}\right) \\ $$$$\mathrm{x}=\:\mathrm{n}\pi+\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{y}}{\mathrm{c}}\right)\:\:\:\:\mathrm{n}\in\mathbb{N} \\ $$
