Question-115645

Question Number 115645 by ZiYangLee last updated on 27/Sep/20

Commented by Dwaipayan Shikari last updated on 27/Sep/20

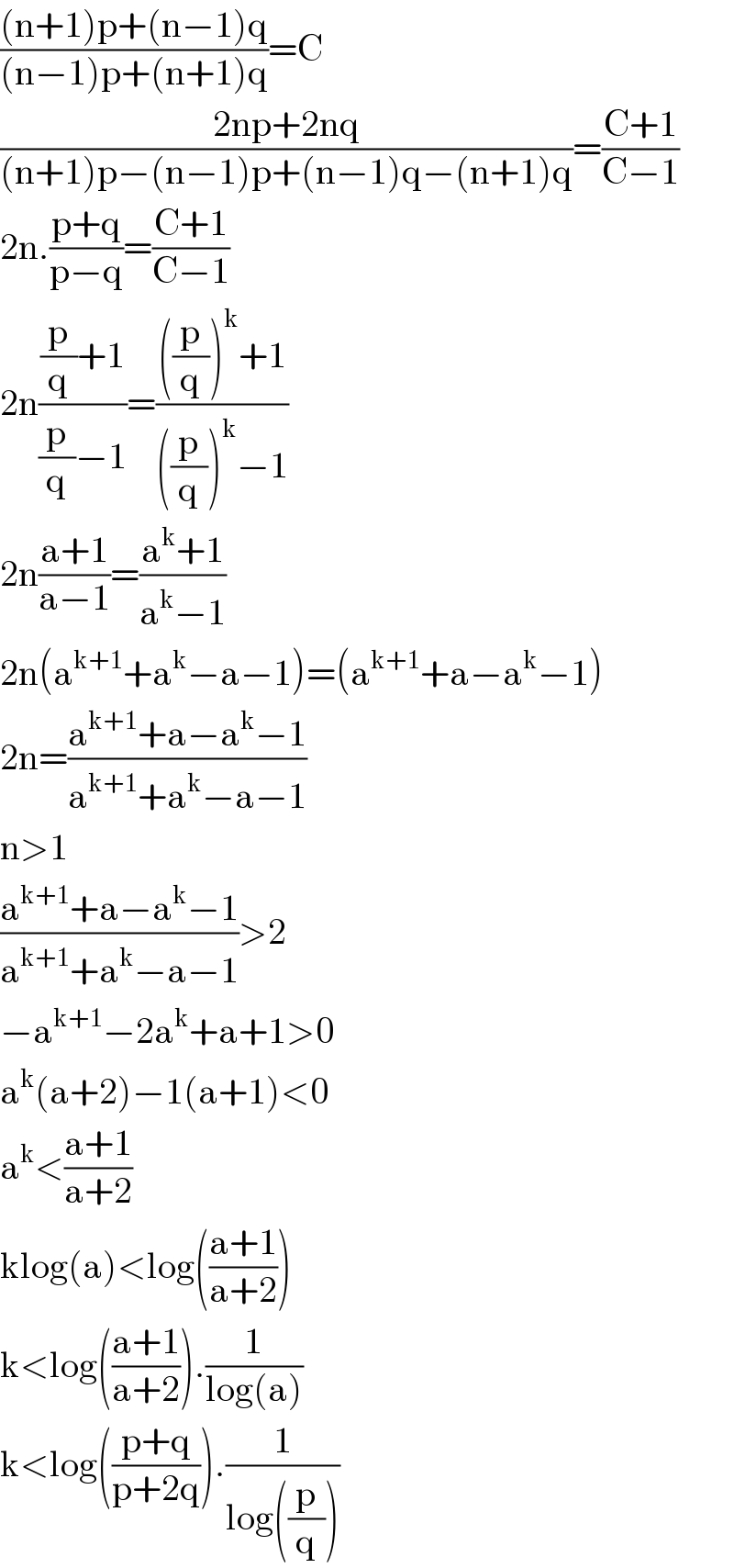
(((n+1)p+(n−1)q)/((n−1)p+(n+1)q))=C ((2np+2nq)/((n+1)p−(n−1)p+(n−1)q−(n+1)q))=((C+1)/(C−1)) 2n.((p+q)/(p−q))=((C+1)/(C−1)) 2n(((p/q)+1)/((p/q)−1))=((((p/q))^k +1)/(((p/q))^k −1)) 2n((a+1)/(a−1))=((a^k +1)/(a^k −1)) 2n(a^(k+1) +a^k −a−1)=(a^(k+1) +a−a^k −1) 2n=((a^(k+1) +a−a^k −1)/(a^(k+1) +a^k −a−1)) n>1 ((a^(k+1) +a−a^k −1)/(a^(k+1) +a^k −a−1))>2 −a^(k+1) −2a^k +a+1>0 a^k (a+2)−1(a+1)<0 a^k <((a+1)/(a+2)) klog(a)<log(((a+1)/(a+2))) k<log(((a+1)/(a+2))).(1/(log(a))) k<log(((p+q)/(p+2q))).(1/(log((p/q))))

$$\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{p}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{q}}{\left(\mathrm{n}−\mathrm{1}\right)\mathrm{p}+\left(\mathrm{n}+\mathrm{1}\right)\mathrm{q}}=\mathrm{C} \\ $$$$\frac{\mathrm{2np}+\mathrm{2nq}}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{p}−\left(\mathrm{n}−\mathrm{1}\right)\mathrm{p}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{q}−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{q}}=\frac{\mathrm{C}+\mathrm{1}}{\mathrm{C}−\mathrm{1}} \\ $$$$\mathrm{2n}.\frac{\mathrm{p}+\mathrm{q}}{\mathrm{p}−\mathrm{q}}=\frac{\mathrm{C}+\mathrm{1}}{\mathrm{C}−\mathrm{1}} \\ $$$$\mathrm{2n}\frac{\frac{\mathrm{p}}{\mathrm{q}}+\mathrm{1}}{\frac{\mathrm{p}}{\mathrm{q}}−\mathrm{1}}=\frac{\left(\frac{\mathrm{p}}{\mathrm{q}}\right)^{\mathrm{k}} +\mathrm{1}}{\left(\frac{\mathrm{p}}{\mathrm{q}}\right)^{\mathrm{k}} −\mathrm{1}} \\ $$$$\mathrm{2n}\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}−\mathrm{1}}=\frac{\mathrm{a}^{\mathrm{k}} +\mathrm{1}}{\mathrm{a}^{\mathrm{k}} −\mathrm{1}} \\ $$$$\mathrm{2n}\left(\mathrm{a}^{\mathrm{k}+\mathrm{1}} +\mathrm{a}^{\mathrm{k}} −\mathrm{a}−\mathrm{1}\right)=\left(\mathrm{a}^{\mathrm{k}+\mathrm{1}} +\mathrm{a}−\mathrm{a}^{\mathrm{k}} −\mathrm{1}\right) \\ $$$$\mathrm{2n}=\frac{\mathrm{a}^{\mathrm{k}+\mathrm{1}} +\mathrm{a}−\mathrm{a}^{\mathrm{k}} −\mathrm{1}}{\mathrm{a}^{\mathrm{k}+\mathrm{1}} +\mathrm{a}^{\mathrm{k}} −\mathrm{a}−\mathrm{1}} \\ $$$$\mathrm{n}>\mathrm{1} \\ $$$$\frac{\mathrm{a}^{\mathrm{k}+\mathrm{1}} +\mathrm{a}−\mathrm{a}^{\mathrm{k}} −\mathrm{1}}{\mathrm{a}^{\mathrm{k}+\mathrm{1}} +\mathrm{a}^{\mathrm{k}} −\mathrm{a}−\mathrm{1}}>\mathrm{2} \\ $$$$−\mathrm{a}^{\mathrm{k}+\mathrm{1}} −\mathrm{2a}^{\mathrm{k}} +\mathrm{a}+\mathrm{1}>\mathrm{0} \\ $$$$\mathrm{a}^{\mathrm{k}} \left(\mathrm{a}+\mathrm{2}\right)−\mathrm{1}\left(\mathrm{a}+\mathrm{1}\right)<\mathrm{0} \\ $$$$\mathrm{a}^{\mathrm{k}} <\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}+\mathrm{2}} \\ $$$$\mathrm{klog}\left(\mathrm{a}\right)<\mathrm{log}\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}+\mathrm{2}}\right) \\ $$$$\mathrm{k}<\mathrm{log}\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}+\mathrm{2}}\right).\frac{\mathrm{1}}{\mathrm{log}\left(\mathrm{a}\right)} \\ $$$$\mathrm{k}<\mathrm{log}\left(\frac{\mathrm{p}+\mathrm{q}}{\mathrm{p}+\mathrm{2q}}\right).\frac{\mathrm{1}}{\mathrm{log}\left(\frac{\mathrm{p}}{\mathrm{q}}\right)} \\ $$

Commented by PRITHWISH SEN 2 last updated on 01/Oct/20

(n+1)p−(n−1)p+(n−1)q−(n+1)q = np+p−np+p+nq−q−np−q = 2(p−q) ∴((2nq+2np)/((n+1)p−(n−1)p+(n−1)q−(n+1)q)) = ((2n(p+q))/(2(p−q))) = ((n(p+q))/((p−q))) please check

$$\left(\mathrm{n}+\mathrm{1}\right)\mathrm{p}−\left(\mathrm{n}−\mathrm{1}\right)\mathrm{p}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{q}−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{q} \\ $$$$=\:\mathrm{np}+\mathrm{p}−\mathrm{np}+\mathrm{p}+\boldsymbol{\mathrm{nq}}−\boldsymbol{\mathrm{q}}−\boldsymbol{\mathrm{np}}−\boldsymbol{\mathrm{q}} \\ $$$$=\:\mathrm{2}\left(\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{q}}\right) \\ $$$$\therefore\frac{\mathrm{2nq}+\mathrm{2np}}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{p}−\left(\mathrm{n}−\mathrm{1}\right)\mathrm{p}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{q}−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{q}} \\ $$$$=\:\frac{\mathrm{2n}\left(\mathrm{p}+\mathrm{q}\right)}{\mathrm{2}\left(\mathrm{p}−\mathrm{q}\right)}\:=\:\frac{\mathrm{n}\left(\mathrm{p}+\mathrm{q}\right)}{\left(\mathrm{p}−\mathrm{q}\right)} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$$$ \\ $$

Answered by PRITHWISH SEN 2 last updated on 27/Sep/20

((n(p+q)+(p−q))/(n(p+q)−(p−q))) = ((p/q))^k ∵p→q⇒(p−q)→0 ((n(p+q))/(n(p+q))) = ((p/q))^k k=0 please check

$$\frac{\mathrm{n}\left(\mathrm{p}+\mathrm{q}\right)+\left(\mathrm{p}−\mathrm{q}\right)}{\mathrm{n}\left(\mathrm{p}+\mathrm{q}\right)−\left(\mathrm{p}−\mathrm{q}\right)}\:=\:\left(\frac{\mathrm{p}}{\mathrm{q}}\right)^{\mathrm{k}} \\ $$$$\because\mathrm{p}\rightarrow\mathrm{q}\Rightarrow\left(\mathrm{p}−\mathrm{q}\right)\rightarrow\mathrm{0} \\ $$$$\frac{\mathrm{n}\left(\mathrm{p}+\mathrm{q}\right)}{\mathrm{n}\left(\mathrm{p}+\mathrm{q}\right)}\:=\:\left(\frac{\mathrm{p}}{\mathrm{q}}\right)^{\mathrm{k}} \\ $$$$\mathrm{k}=\mathrm{0}\:\mathrm{please}\:\mathrm{check} \\ $$

Commented by ZiYangLee last updated on 27/Sep/20

$${But}\:{p}\:{is}\:{just}\:{approximately}\:{equal} \\ $$$${to}\:{q},\:{i}\:{think}\:{we}\:{cannot}\:{assume}\:{that} \\ $$$${p}\:{is}\:{equal}\:{to}\:{q}……{hmmm} \\ $$

Commented by PRITHWISH SEN 2 last updated on 27/Sep/20

that is why I have written p−q→0 not as p−q=0

$$\mathrm{that}\:\mathrm{is}\:\mathrm{why}\:\mathrm{I}\:\mathrm{have}\:\mathrm{written} \\ $$$$\mathrm{p}−\mathrm{q}\rightarrow\mathrm{0}\:\mathrm{not}\:\mathrm{as}\:\mathrm{p}−\mathrm{q}=\mathrm{0} \\ $$

Commented by PRITHWISH SEN 2 last updated on 27/Sep/20

now if p−q=ε ε= a very small positive quantity then n(p+q)+ε → n(p+q)−ε ∴ ((n(p+q)+ε)/(n(p+q)−ε)) → 1 I think

$$\mathrm{now}\:\mathrm{if}\:\mathrm{p}−\mathrm{q}=\epsilon\:\:\epsilon=\:\mathrm{a}\:\mathrm{very}\:\mathrm{small}\:\mathrm{positive}\:\mathrm{quantity} \\ $$$$\mathrm{then}\:\mathrm{n}\left(\mathrm{p}+\mathrm{q}\right)+\epsilon\:\rightarrow\:\mathrm{n}\left(\mathrm{p}+\mathrm{q}\right)−\epsilon \\ $$$$\therefore\:\frac{\mathrm{n}\left(\mathrm{p}+\mathrm{q}\right)+\epsilon}{\mathrm{n}\left(\mathrm{p}+\mathrm{q}\right)−\epsilon}\:\rightarrow\:\mathrm{1}\:\:\:\mathrm{I}\:\mathrm{think} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply