Question Number 115943 by A8;15: last updated on 29/Sep/20

Commented by A8;15: last updated on 29/Sep/20
thanks sir
Commented by mathdave last updated on 29/Sep/20

Commented by mathdave last updated on 29/Sep/20

Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Answered by TANMAY PANACEA last updated on 29/Sep/20
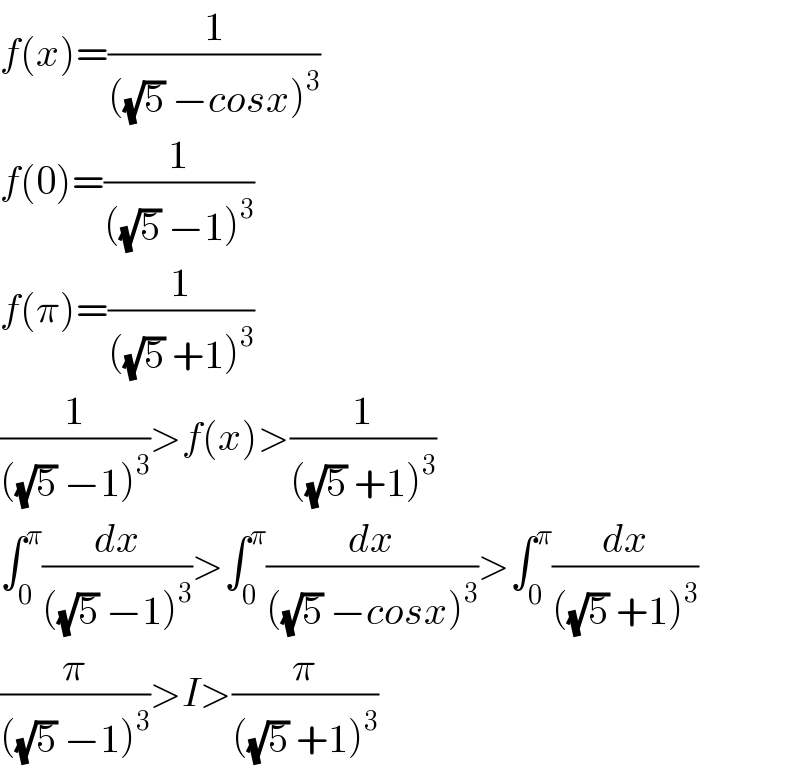
$${f}\left({x}\right)=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{5}}\:−{cosx}\right)^{\mathrm{3}} } \\ $$$${f}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${f}\left(\pi\right)=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{5}}\:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\frac{\mathrm{1}}{\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right)^{\mathrm{3}} }>{f}\left({x}\right)>\frac{\mathrm{1}}{\left(\sqrt{\mathrm{5}}\:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right)^{\mathrm{3}} }>\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left(\sqrt{\mathrm{5}}\:−{cosx}\right)^{\mathrm{3}} }>\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left(\sqrt{\mathrm{5}}\:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\frac{\pi}{\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right)^{\mathrm{3}} }>{I}>\frac{\pi}{\left(\sqrt{\mathrm{5}}\:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$
Commented by A8;15: last updated on 29/Sep/20
thanks sir
Answered by maths mind last updated on 29/Sep/20

$$\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left(\sqrt{\mathrm{5}}−{cos}\left({x}\right)\right)^{\mathrm{3}} }=\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left(\sqrt{\mathrm{5}}+{cos}\left({x}\right)\right)^{\mathrm{3}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left(\sqrt{\mathrm{5}}−{cos}\left({x}\right)\right)^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{dx}}{\left(\sqrt{\mathrm{5}}+{cos}\left({x}\right)\right)^{\mathrm{3}} } \\ $$$${cos}\left({x}\right)=\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{8}{e}^{\mathrm{3}{ix}} }{\left(\sqrt{\mathrm{5}}{e}^{{ix}} +{e}^{\mathrm{2}{ix}} +\mathrm{1}\right)^{\mathrm{3}} }{dx} \\ $$$${z}={e}^{{ix}} \Rightarrow{dz}={ie}^{{ix}} {dx} \\ $$$$=\frac{\mathrm{4}}{{i}}\int_{{C}} \frac{{z}^{\mathrm{2}} }{\left({z}^{\mathrm{2}} +\sqrt{\mathrm{5}}{z}+\mathrm{1}\right)^{\mathrm{3}} },{C}\:{unite}\:{circl} \\ $$$$=\frac{\mathrm{4}}{{i}}\int_{{C}} \frac{{z}^{\mathrm{2}} }{\left({z}−\left(\frac{−\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\underset{={z}_{\mathrm{1}} } {\right)}\right)\left({z}−\left(\frac{−\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\underset{=\underset{\mathrm{2}} {{z}}} {\right)}\right)} \\ $$$$={only}\:\frac{−\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\in{C} \\ $$$$=\mathrm{8}\pi{Res}\left(\frac{{z}^{\mathrm{2}} }{\left({z}−{z}_{\mathrm{1}} \right)^{\mathrm{3}} \left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} }\mid_{{z}_{\mathrm{2}} } \right) \\ $$$$ \\ $$
Commented by A8;15: last updated on 29/Sep/20
thanks
Answered by mathmax by abdo last updated on 29/Sep/20

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{a}−\mathrm{cosx}}\:\:\mathrm{with}\:\mathrm{a}>\mathrm{1}\:\mathrm{we}\:\mathrm{havef}^{'} \left(\mathrm{a}\right)=−\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dx}}{\left(\mathrm{a}−\mathrm{cosx}\right)^{\mathrm{2}} } \\ $$$$\mathrm{and}\:\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{2}\left(\mathrm{a}−\mathrm{cosx}\right)}{\left(\mathrm{a}−\mathrm{cosx}\right)^{\mathrm{4}} }\:\mathrm{dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{a}−\mathrm{cosx}\right)^{\mathrm{3}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\left(\sqrt{\mathrm{5}}−\mathrm{cosx}\right)^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{f}^{\left(\mathrm{2}\right)} \left(\sqrt{\mathrm{5}}\right)\:\:\mathrm{let}\:\mathrm{explicit}\:\mathrm{f}\left(\mathrm{a}\right) \\ $$$$\mathrm{changement}\:\mathrm{t}\:=\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{give}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{a}−\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{a}+\mathrm{at}^{\mathrm{2}} −\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\left(\mathrm{a}+\mathrm{1}\right)\mathrm{t}^{\mathrm{2}} +\mathrm{a}−\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{a}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}\:=_{\mathrm{t}\:=\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}\mathrm{u}} \:\:\frac{\mathrm{2}}{\mathrm{a}+\mathrm{1}}.\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}−\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\frac{\sqrt{\mathrm{a}−\mathrm{1}}}{\:\sqrt{\mathrm{a}+\mathrm{1}}}\mathrm{du} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\:\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\pi\left\{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}^{\left(\mathrm{1}\right)} \\ $$$$=\pi\left(−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2a}\right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \right)=−\pi\mathrm{a}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{f}^{''} \left(\mathrm{a}\right)\:=−\pi\left\{\:\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:+\mathrm{a}\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\mathrm{2a}\right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{5}}{\mathrm{2}}} \right\} \\ $$$$=−\pi\left\{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{3a}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{5}}{\mathrm{2}}} \right\}\Rightarrow \\ $$$$\mathrm{f}^{''} \left(\sqrt{\mathrm{5}}\right)\:=−\pi\left\{\:\mathrm{4}^{−\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{15}\left(\mathrm{4}\right)^{−\frac{\mathrm{5}}{\mathrm{2}}} \right\} \\ $$$$=−\frac{\pi}{\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:+\frac{\mathrm{15}\pi}{\mathrm{4}^{\frac{\mathrm{5}}{\mathrm{2}}} }\:=−\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{15}\pi}{\mathrm{32}}\:=\frac{−\mathrm{4}\pi\:+\mathrm{15}\pi}{\mathrm{32}}\:=\frac{\mathrm{11}\pi}{\mathrm{32}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\left(\sqrt{\mathrm{5}}−\mathrm{cosx}\right)^{\mathrm{3}} }\:=\frac{\mathrm{11}\pi}{\mathrm{64}} \\ $$
Answered by MJS_new last updated on 30/Sep/20
![∫_0 ^π (dx/((a−cos x)^3 ))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =(2/((a+1)^3 ))∫_0 ^∞ (((t^2 +1)^2 )/((t^2 +((a−1)/(a+1)))^3 ))dt= [b=((a−1)/(a+1))] =(2/((a+1)^3 ))∫_0 ^∞ (((t^2 +1)^2 )/((t^2 +b)^3 ))dt= [Ostrogradski] =[−(((b−1)t((5b+3)t^2 +b(3b+5)))/(4(a+1)^3 b^2 (t^2 +b)^2 ))]_0 ^∞ + +((3b^2 +2b+3)/(4(a+1)^3 b^2 ))∫_0 ^∞ (dt/(t^2 +b)) obviously the first part is equal to zero ((3b^2 +2b+3)/(4(a+1)^3 b^2 ))∫_0 ^∞ (dt/(t^2 +b))= =[((3b^2 +2b+3)/(4(a+1)^3 b^(5/2) ))arctan (t/( (√b)))]_0 ^∞ = =((3b^2 +2b+3)/(8(a+1)^3 b^(5/2) ))π= =((2a^2 +1)/(2(a^2 −1)^(5/2) ))π= =((11)/(64))π](https://www.tinkutara.com/question/Q115987.png)
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{dx}}{\left({a}−\mathrm{cos}\:{x}\right)^{\mathrm{3}} }= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\frac{\mathrm{2}}{\left({a}+\mathrm{1}\right)^{\mathrm{3}} }\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}\right)^{\mathrm{3}} }{dt}= \\ $$$$\:\:\:\:\:\left[{b}=\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}\right] \\ $$$$=\frac{\mathrm{2}}{\left({a}+\mathrm{1}\right)^{\mathrm{3}} }\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +{b}\right)^{\mathrm{3}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=\left[−\frac{\left({b}−\mathrm{1}\right){t}\left(\left(\mathrm{5}{b}+\mathrm{3}\right){t}^{\mathrm{2}} +{b}\left(\mathrm{3}{b}+\mathrm{5}\right)\right)}{\mathrm{4}\left({a}+\mathrm{1}\right)^{\mathrm{3}} {b}^{\mathrm{2}} \left({t}^{\mathrm{2}} +{b}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\infty} + \\ $$$$\:\:\:\:\:+\frac{\mathrm{3}{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{3}}{\mathrm{4}\left({a}+\mathrm{1}\right)^{\mathrm{3}} {b}^{\mathrm{2}} }\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +{b}} \\ $$$$\mathrm{obviously}\:\mathrm{the}\:\mathrm{first}\:\mathrm{part}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{zero} \\ $$$$\frac{\mathrm{3}{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{3}}{\mathrm{4}\left({a}+\mathrm{1}\right)^{\mathrm{3}} {b}^{\mathrm{2}} }\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +{b}}= \\ $$$$=\left[\frac{\mathrm{3}{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{3}}{\mathrm{4}\left({a}+\mathrm{1}\right)^{\mathrm{3}} {b}^{\mathrm{5}/\mathrm{2}} }\mathrm{arctan}\:\frac{{t}}{\:\sqrt{{b}}}\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=\frac{\mathrm{3}{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{3}}{\mathrm{8}\left({a}+\mathrm{1}\right)^{\mathrm{3}} {b}^{\mathrm{5}/\mathrm{2}} }\pi= \\ $$$$=\frac{\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{5}/\mathrm{2}} }\pi= \\ $$$$=\frac{\mathrm{11}}{\mathrm{64}}\pi \\ $$
