Menu Close

Question-115961

Tinku Tara 0 Comments
Pin




Question Number 115961 by Ar Brandon last updated on 29/Sep/20
Commented by Dwaipayan Shikari last updated on 29/Sep/20
Indetermined
$$\mathrm{Indetermined} \\ $$
Commented by Ar Brandon last updated on 29/Sep/20
Have you taken note of the sign ? When x approaches 0 from below. Doesn't it make a difference ?
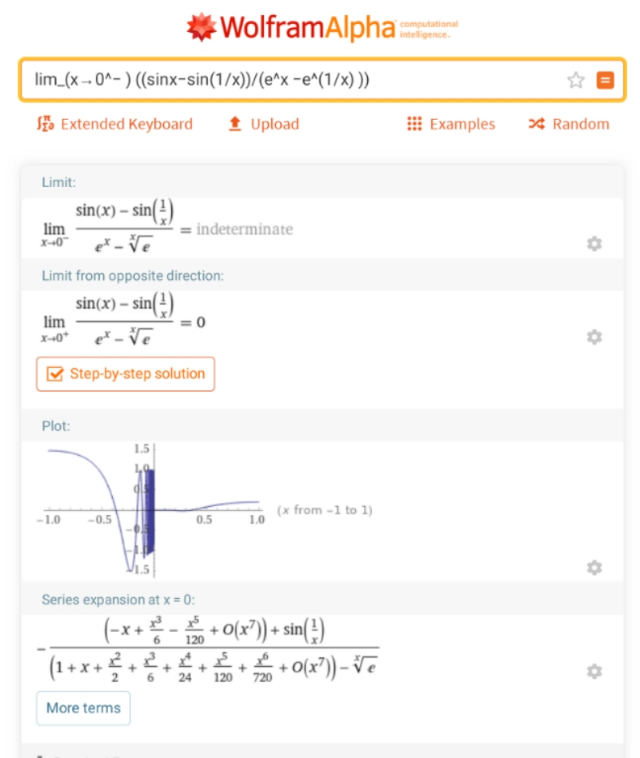
Commented by Dwaipayan Shikari last updated on 29/Sep/20
Commented by Ar Brandon last updated on 29/Sep/20
I tried using MacLaurine's expansion. But not very sure of my result. My solution is as follows :
Commented by Ar Brandon last updated on 29/Sep/20
L=lim_(x→−0) ((sinx−sin((1/x)))/(e^x −e^(1/x) )) sinx≈x−(x^3 /(3!))⇒sin((1/x))≈(1/x)−(1/(3!x^3 )) e^x ≈1+x+(x^2 /(2!))+(x^3 /(3!))⇒e^(1/x) ≈1+(1/x)+(1/(2!x^2 ))+(1/(3!x^3 )) ⇒L=lim_(x→−0) (({x−(x^3 /(3!))}−{(1/x)−(1/(3!x^3 ))})/({1+x+(x^2 /(2!))+(x^3 /(3!))}−{1+(1/x)+(1/(2!x^2 ))+(1/(3!x^3 ))})) =lim_(x→0) (({x^4 −(x^6 /(3!))}−{x^2 −(1/(3!))})/({x^4 +(x^5 /(2!))+(x^6 /(3!))}−{x^2 +(x/(2!))+(1/(3!))}))=−(1/(3!))÷(1/(3!))=−1
$$\mathscr{L}=\underset{{x}\rightarrow−\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}{x}−\mathrm{sin}\left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{e}^{{x}} −\mathrm{e}^{\frac{\mathrm{1}}{{x}}} } \\ $$$$\mathrm{sin}{x}\approx{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\Rightarrow\mathrm{sin}\left(\frac{\mathrm{1}}{{x}}\right)\approx\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{3}!{x}^{\mathrm{3}} } \\ $$$$\mathrm{e}^{{x}} \approx\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\Rightarrow\mathrm{e}^{\frac{\mathrm{1}}{{x}}} \approx\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}!{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}!{x}^{\mathrm{3}} } \\ $$$$\Rightarrow\mathscr{L}=\underset{{x}\rightarrow−\mathrm{0}} {\mathrm{lim}}\frac{\left\{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right\}−\left\{\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{3}!{x}^{\mathrm{3}} }\right\}}{\left\{\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right\}−\left\{\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}!{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}!{x}^{\mathrm{3}} }\right\}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left\{{x}^{\mathrm{4}} −\frac{{x}^{\mathrm{6}} }{\mathrm{3}!}\right\}−\left\{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}!}\right\}}{\left\{{x}^{\mathrm{4}} +\frac{{x}^{\mathrm{5}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{6}} }{\mathrm{3}!}\right\}−\left\{{x}^{\mathrm{2}} +\frac{{x}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}\right\}}=−\frac{\mathrm{1}}{\mathrm{3}!}\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{3}!}=−\mathrm{1} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Sep/20
It is 3.14 =π am in India , now I have to sleep ����
Commented by Ar Brandon last updated on 29/Sep/20
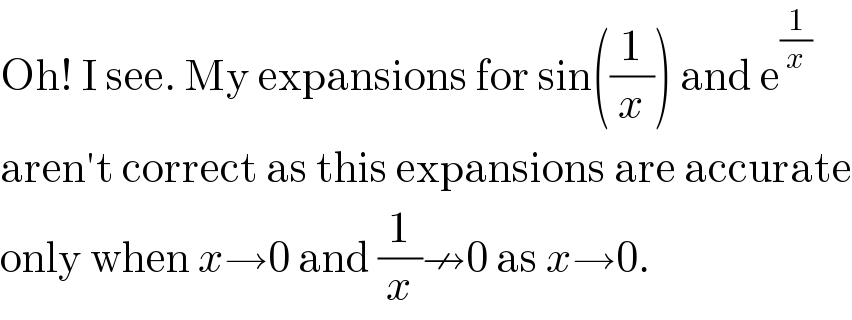
Oh! I see. My expansions for sin((1/x)) and e^(1/x) aren′t correct as this expansions are accurate only when x→0 and (1/x)↛0 as x→0.
$$\mathrm{Oh}!\:\mathrm{I}\:\mathrm{see}.\:\mathrm{My}\:\mathrm{expansions}\:\mathrm{for}\:\mathrm{sin}\left(\frac{\mathrm{1}}{{x}}\right)\:\mathrm{and}\:\mathrm{e}^{\frac{\mathrm{1}}{{x}}} \\ $$$$\mathrm{aren}'\mathrm{t}\:\mathrm{correct}\:\mathrm{as}\:\mathrm{this}\:\mathrm{expansions}\:\mathrm{are}\:\mathrm{accurate} \\ $$$$\mathrm{only}\:\mathrm{when}\:{x}\rightarrow\mathrm{0}\:\mathrm{and}\:\frac{\mathrm{1}}{{x}}\nrightarrow\mathrm{0}\:\mathrm{as}\:{x}\rightarrow\mathrm{0}. \\ $$
Commented by Ar Brandon last updated on 30/Sep/20
Good Night��
Answered by Ar Brandon last updated on 30/Sep/20
L=lim_(x→0) ((sinx−sin((1/x)))/(e^x −e^(1/x) )) sinx≈x−(x^3 /(3!)) , e^x ≈1+x+(x^2 /(2!))+(x^3 /(3!)) ⇒L=lim_(x→0) (({x−(x^3 /(3!))}−sin((1/x)))/({1+x+(x^2 /(2!))+(x^3 /(3!))}−e^(1/x) ))=lim_(x→0) ((−sin((1/x)))/(1−e^(1/x) )) u=(1/x), x→+0 ⇒ u→+∞ , x→−0 ⇒ u→−∞ ⇒lim_(x→+0) ((−sin((1/x)))/(1−e^(1/x) ))=lim_(u→+∞) ((−sin(u))/(1−e^u ))=((−sin(u))/(−∞))=0 {−1≤sin(u)≤1} ⇒lim_(x→−0) ((−sin((1/x)))/(1−e^(1/x) ))=lim_(u→−∞) ((−sin(u))/(1−e^u ))=((−sin(u))/(1−0))=[−1;1] (indetermined)
$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}{x}−\mathrm{sin}\left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{e}^{{x}} −\mathrm{e}^{\frac{\mathrm{1}}{{x}}} } \\ $$$$\mathrm{sin}{x}\approx{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:,\:\mathrm{e}^{{x}} \approx\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!} \\ $$$$\Rightarrow\mathscr{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left\{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right\}−\mathrm{sin}\left(\frac{\mathrm{1}}{{x}}\right)}{\left\{\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right\}−\mathrm{e}^{\frac{\mathrm{1}}{{x}}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{sin}\left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{1}−\mathrm{e}^{\frac{\mathrm{1}}{{x}}} } \\ $$$$\mathrm{u}=\frac{\mathrm{1}}{{x}},\:{x}\rightarrow+\mathrm{0}\:\Rightarrow\:\mathrm{u}\rightarrow+\infty\:,\:{x}\rightarrow−\mathrm{0}\:\Rightarrow\:\mathrm{u}\rightarrow−\infty \\ $$$$\Rightarrow\underset{{x}\rightarrow+\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{sin}\left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{1}−\mathrm{e}^{\frac{\mathrm{1}}{{x}}} }=\underset{\mathrm{u}\rightarrow+\infty} {\mathrm{lim}}\frac{−\mathrm{sin}\left(\mathrm{u}\right)}{\mathrm{1}−\mathrm{e}^{\mathrm{u}} }=\frac{−\mathrm{sin}\left(\mathrm{u}\right)}{−\infty}=\mathrm{0}\:\left\{−\mathrm{1}\leqslant\mathrm{sin}\left(\mathrm{u}\right)\leqslant\mathrm{1}\right\} \\ $$$$\Rightarrow\underset{{x}\rightarrow−\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{sin}\left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{1}−\mathrm{e}^{\frac{\mathrm{1}}{{x}}} }=\underset{\mathrm{u}\rightarrow−\infty} {\mathrm{lim}}\frac{−\mathrm{sin}\left(\mathrm{u}\right)}{\mathrm{1}−\mathrm{e}^{\mathrm{u}} }=\frac{−\mathrm{sin}\left(\mathrm{u}\right)}{\mathrm{1}−\mathrm{0}}=\left[−\mathrm{1};\mathrm{1}\right]\:\left(\mathrm{indetermined}\right) \\ $$
Answered by maths mind last updated on 30/Sep/20
x=(1/(2kπ+α)),k→−∞⇒x→0^− ,withe α∈[−(π/2),(π/2)] ((sin(x)−sin((1/x)))/(e^x −e^(1/x) ))=((sin((1/(2kπ+α)))−sin(2kπ+α))/(e^(1/(2kπ+α)) −e^(2kπ+α) )) sin(2kπ)=0,∀k∈Z e^(1/(2kπ+α)) −e^(2kπ+α) →1 sin((1/(2kπ+α)))→0 sin(2kπ+α)=sin(α) we get −sin(α) depend in α ⇒ not unique Limite no limite
$${x}=\frac{\mathrm{1}}{\mathrm{2}{k}\pi+\alpha},{k}\rightarrow−\infty\Rightarrow{x}\rightarrow\mathrm{0}^{−} ,{withe}\:\alpha\in\left[−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right] \\ $$$$\frac{{sin}\left({x}\right)−{sin}\left(\frac{\mathrm{1}}{{x}}\right)}{{e}^{{x}} −{e}^{\frac{\mathrm{1}}{{x}}} }=\frac{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}{k}\pi+\alpha}\right)−{sin}\left(\mathrm{2}{k}\pi+\alpha\right)}{{e}^{\frac{\mathrm{1}}{\mathrm{2}{k}\pi+\alpha}} −{e}^{\mathrm{2}{k}\pi+\alpha} } \\ $$$${sin}\left(\mathrm{2}{k}\pi\right)=\mathrm{0},\forall{k}\in\mathbb{Z} \\ $$$${e}^{\frac{\mathrm{1}}{\mathrm{2}{k}\pi+\alpha}} −{e}^{\mathrm{2}{k}\pi+\alpha} \rightarrow\mathrm{1} \\ $$$${sin}\left(\frac{\mathrm{1}}{\mathrm{2}{k}\pi+\alpha}\right)\rightarrow\mathrm{0}\:{sin}\left(\mathrm{2}{k}\pi+\alpha\right)={sin}\left(\alpha\right) \\ $$$${we}\:{get}\:−{sin}\left(\alpha\right) \\ $$$${depend}\:{in}\:\alpha\:\Rightarrow\:{not}\:{unique}\:{Limite}\: \\ $$$${no}\:{limite} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *