Question-115968

Question Number 115968 by Engr_Jidda last updated on 29/Sep/20

Answered by 1549442205PVT last updated on 30/Sep/20

Put u(x,y)=x^2 −1;v(x,y)=y^2 +1 The condition Cauchy−Rieman for the analytical is (∂u/∂x)=(∂v/∂y)(1),(∂u/∂y)=−(∂v/∂x)(2) We have (∂u/∂x)=2x,(∂u/∂y)=0,(∂v/∂x)=0,(∂v/∂y)=2y Henece,we need must have 2x=2y(second condition is satisfied ∀x,y)⇔y=x Thus,f(z) is analytical function on the line y=x and we have : f ′(z)=(∂u/∂x)+i(∂v/∂x)=(∂u/∂x)−i(∂u/∂y)=(∂v/∂y)−i(∂u/∂y)=(∂v/∂y)+i(∂v/∂x) =2x=2y

$$\mathrm{Put}\:\mathrm{u}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{1};\mathrm{v}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{y}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{The}\:\mathrm{condition}\:\mathrm{Cauchy}−\mathrm{Rieman}\:\mathrm{for} \\ $$$$\mathrm{the}\:\mathrm{analytical}\:\mathrm{is}\:\frac{\partial\mathrm{u}}{\partial\mathrm{x}}=\frac{\partial\mathrm{v}}{\partial\mathrm{y}}\left(\mathrm{1}\right),\frac{\partial\mathrm{u}}{\partial\mathrm{y}}=−\frac{\partial\mathrm{v}}{\partial\mathrm{x}}\left(\mathrm{2}\right) \\ $$$$\mathrm{We}\:\mathrm{have}\:\frac{\partial\mathrm{u}}{\partial\mathrm{x}}=\mathrm{2x},\frac{\partial\mathrm{u}}{\partial\mathrm{y}}=\mathrm{0},\frac{\partial\mathrm{v}}{\partial\mathrm{x}}=\mathrm{0},\frac{\partial\mathrm{v}}{\partial\mathrm{y}}=\mathrm{2y} \\ $$$$\mathrm{Henece},\mathrm{we}\:\mathrm{need}\:\mathrm{must}\:\mathrm{have} \\ $$$$\mathrm{2x}=\mathrm{2y}\left(\mathrm{second}\:\mathrm{condition}\:\mathrm{is}\:\mathrm{satisfied}\right. \\ $$$$\left.\forall\mathrm{x},\mathrm{y}\right)\Leftrightarrow\mathrm{y}=\mathrm{x} \\ $$$$\mathrm{Thus},\mathrm{f}\left(\mathrm{z}\right)\:\mathrm{is}\:\mathrm{analytical}\:\mathrm{function} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{x}\:\mathrm{and}\:\mathrm{we}\:\mathrm{have}\:: \\ $$$$\mathrm{f}\:'\left(\mathrm{z}\right)=\frac{\partial\mathrm{u}}{\partial\mathrm{x}}+\mathrm{i}\frac{\partial\mathrm{v}}{\partial\mathrm{x}}=\frac{\partial\mathrm{u}}{\partial\mathrm{x}}−\mathrm{i}\frac{\partial\mathrm{u}}{\partial\mathrm{y}}=\frac{\partial\mathrm{v}}{\partial\mathrm{y}}−\mathrm{i}\frac{\partial\mathrm{u}}{\partial\mathrm{y}}=\frac{\partial\mathrm{v}}{\partial\mathrm{y}}+\mathrm{i}\frac{\partial\mathrm{v}}{\partial\mathrm{x}} \\ $$$$=\mathrm{2x}=\mathrm{2y} \\ $$

Commented by Engr_Jidda last updated on 30/Sep/20

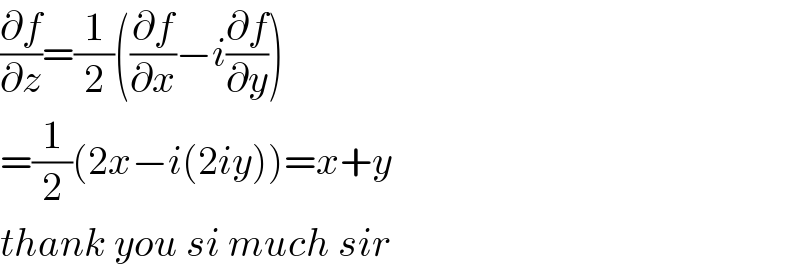
(∂f/∂z)=(1/2)((∂f/∂x)−i(∂f/∂y)) =(1/2)(2x−i(2iy))=x+y thank you si much sir

$$\frac{\partial{f}}{\partial{z}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\partial{f}}{\partial{x}}−{i}\frac{\partial{f}}{\partial{y}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}−{i}\left(\mathrm{2}{iy}\right)\right)={x}+{y} \\ $$$${thank}\:{you}\:{si}\:{much}\:{sir} \\ $$

Commented by Engr_Jidda last updated on 30/Sep/20

$${thank}\:{you}\:{very}\:{much}\:{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply