Question Number 116114 by Khalmohmmad last updated on 01/Oct/20

Answered by Dwaipayan Shikari last updated on 01/Oct/20
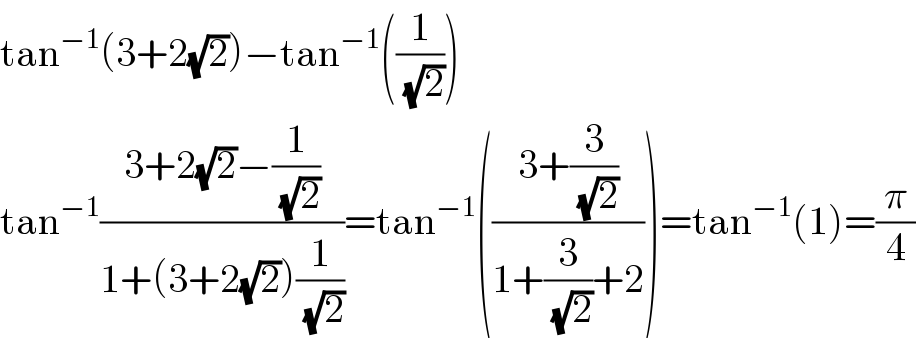
$$\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}+\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}+\mathrm{2}}\right)=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}} \\ $$
