Question Number 116192 by bemath last updated on 01/Oct/20

Commented by MJS_new last updated on 01/Oct/20

$${x}={y}={z}=\mathrm{0} \\ $$$$\mathrm{not}\:\mathrm{sure}\:\mathrm{how}\:\mathrm{to}\:\mathrm{further}\:\mathrm{solve}\:\mathrm{it} \\ $$
Answered by TANMAY PANACEA last updated on 01/Oct/20
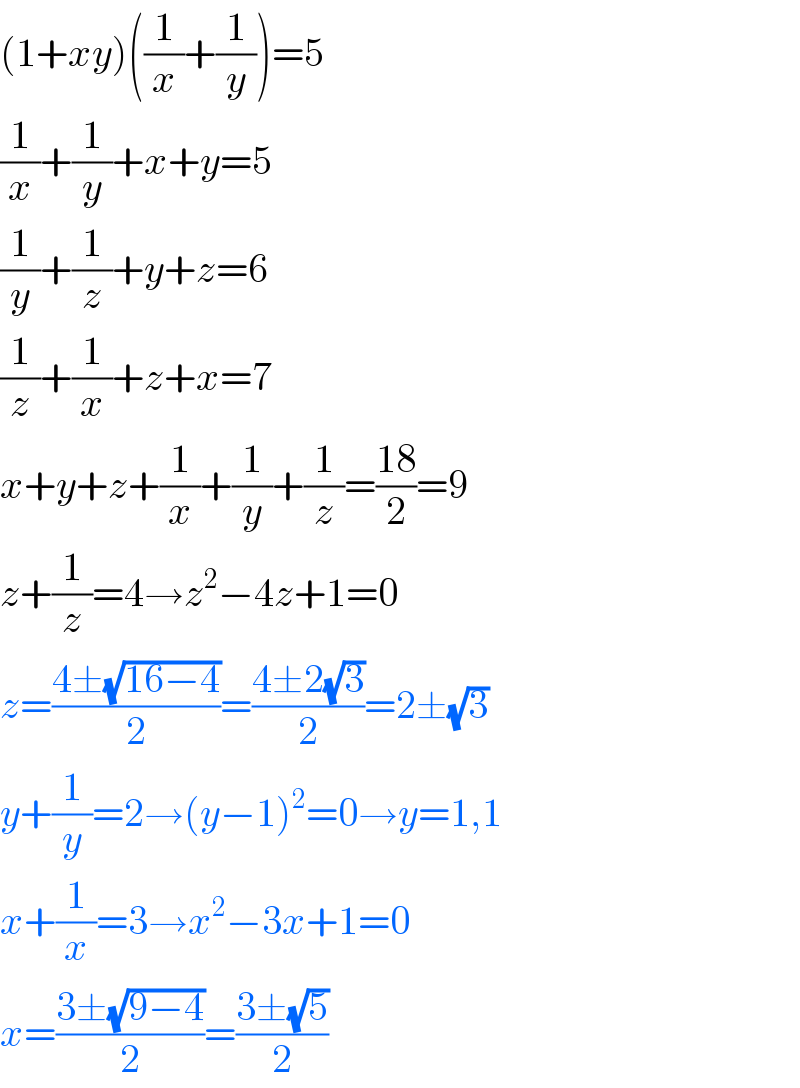
$$\left(\mathrm{1}+{xy}\right)\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\right)=\mathrm{5} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+{x}+{y}=\mathrm{5} \\ $$$$\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}+{y}+{z}=\mathrm{6} \\ $$$$\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{{x}}+{z}+{x}=\mathrm{7} \\ $$$${x}+{y}+{z}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{18}}{\mathrm{2}}=\mathrm{9} \\ $$$${z}+\frac{\mathrm{1}}{{z}}=\mathrm{4}\rightarrow{z}^{\mathrm{2}} −\mathrm{4}{z}+\mathrm{1}=\mathrm{0} \\ $$$${z}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{3}}\: \\ $$$${y}+\frac{\mathrm{1}}{{y}}=\mathrm{2}\rightarrow\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\rightarrow{y}=\mathrm{1},\mathrm{1} \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{3}\rightarrow{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 01/Oct/20

$$\mathrm{great}! \\ $$
Commented by TANMAY PANACEA last updated on 01/Oct/20

$${thank}\:{you}\:{sir} \\ $$
Answered by bobhans last updated on 02/Oct/20

