Question Number 116347 by Khalmohmmad last updated on 03/Oct/20
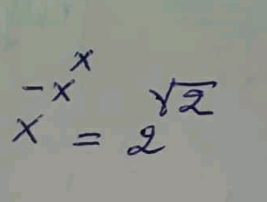
Answered by MJS_new last updated on 03/Oct/20
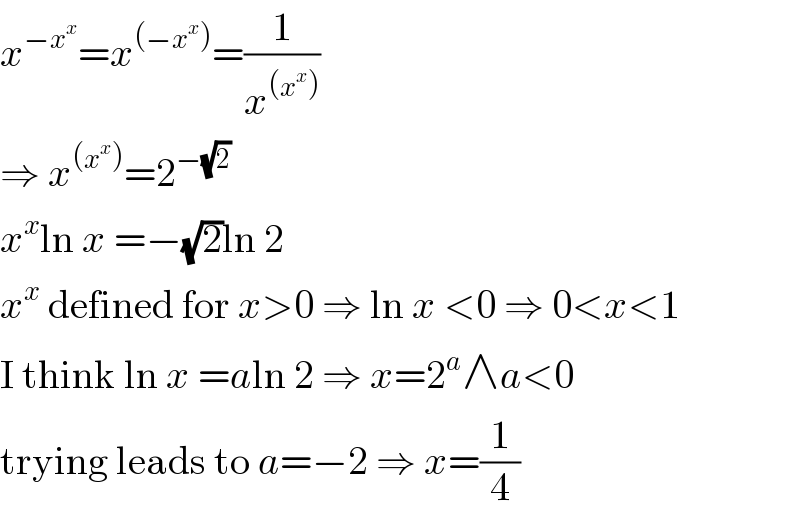
$${x}^{−{x}^{{x}} } ={x}^{\left(−{x}^{{x}} \right)} =\frac{\mathrm{1}}{{x}^{\left({x}^{{x}} \right)} } \\ $$$$\Rightarrow\:{x}^{\left({x}^{{x}} \right)} =\mathrm{2}^{−\sqrt{\mathrm{2}}} \\ $$$${x}^{{x}} \mathrm{ln}\:{x}\:=−\sqrt{\mathrm{2}}\mathrm{ln}\:\mathrm{2} \\ $$$${x}^{{x}} \:\mathrm{defined}\:\mathrm{for}\:{x}>\mathrm{0}\:\Rightarrow\:\mathrm{ln}\:{x}\:<\mathrm{0}\:\Rightarrow\:\mathrm{0}<{x}<\mathrm{1} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{ln}\:{x}\:={a}\mathrm{ln}\:\mathrm{2}\:\Rightarrow\:{x}=\mathrm{2}^{{a}} \wedge{a}<\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{leads}\:\mathrm{to}\:{a}=−\mathrm{2}\:\Rightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
