Question-116361

Question Number 116361 by mohammad17 last updated on 03/Oct/20

Commented by mohammad17 last updated on 03/Oct/20

$${prove}\:{that} \\ $$

Answered by maths mind last updated on 05/Oct/20

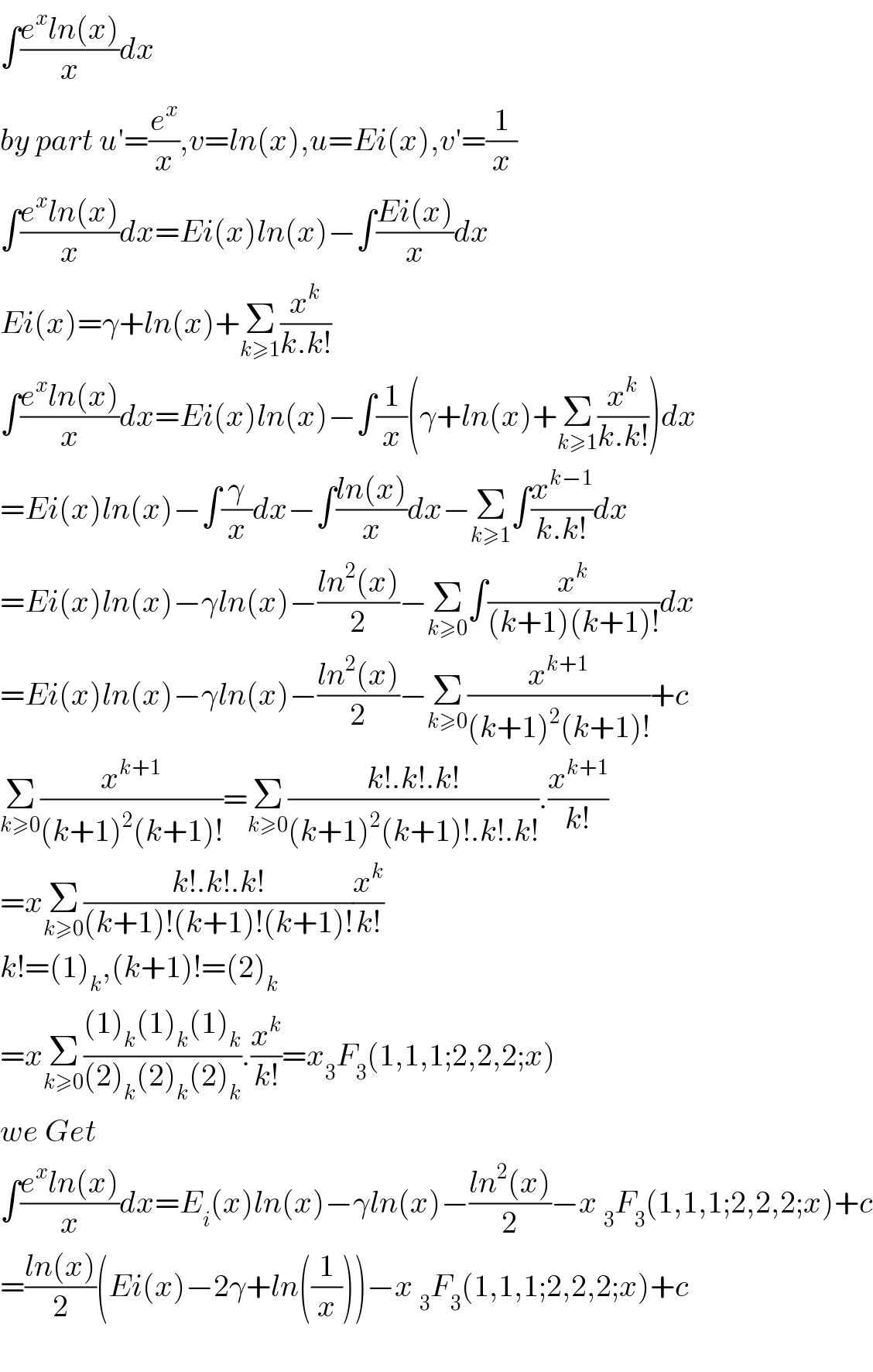
∫((e^x ln(x))/x)dx by part u′=(e^x /x),v=ln(x),u=Ei(x),v′=(1/x) ∫((e^x ln(x))/x)dx=Ei(x)ln(x)−∫((Ei(x))/x)dx Ei(x)=γ+ln(x)+Σ_(k≥1) (x^k /(k.k!)) ∫((e^x ln(x))/x)dx=Ei(x)ln(x)−∫(1/x)(γ+ln(x)+Σ_(k≥1) (x^k /(k.k!)))dx =Ei(x)ln(x)−∫(γ/x)dx−∫((ln(x))/x)dx−Σ_(k≥1) ∫(x^(k−1) /(k.k!))dx =Ei(x)ln(x)−γln(x)−((ln^2 (x))/2)−Σ_(k≥0) ∫(x^k /((k+1)(k+1)!))dx =Ei(x)ln(x)−γln(x)−((ln^2 (x))/2)−Σ_(k≥0) (x^(k+1) /((k+1)^2 (k+1)!))+c Σ_(k≥0) (x^(k+1) /((k+1)^2 (k+1)!))=Σ_(k≥0) ((k!.k!.k!)/((k+1)^2 (k+1)!.k!.k!)).(x^(k+1) /(k!)) =xΣ_(k≥0) ((k!.k!.k!)/((k+1)!(k+1)!(k+1)!))(x^k /(k!)) k!=(1)_k ,(k+1)!=(2)_k =xΣ_(k≥0) (((1)_k (1)_k (1)_k )/((2)_k (2)_k (2)_k )).(x^k /(k!))=x_3 F_3 (1,1,1;2,2,2;x) we Get ∫((e^x ln(x))/x)dx=E_i (x)ln(x)−γln(x)−((ln^2 (x))/2)−x _3 F_3 (1,1,1;2,2,2;x)+c =((ln(x))/2)(Ei(x)−2γ+ln((1/x)))−x _3 F_3 (1,1,1;2,2,2;x)+c

$$\int\frac{{e}^{{x}} {ln}\left({x}\right)}{{x}}{dx} \\ $$$${by}\:{part}\:{u}'=\frac{{e}^{{x}} }{{x}},{v}={ln}\left({x}\right),{u}={Ei}\left({x}\right),{v}'=\frac{\mathrm{1}}{{x}} \\ $$$$\int\frac{{e}^{{x}} {ln}\left({x}\right)}{{x}}{dx}={Ei}\left({x}\right){ln}\left({x}\right)−\int\frac{{Ei}\left({x}\right)}{{x}}{dx} \\ $$$${Ei}\left({x}\right)=\gamma+{ln}\left({x}\right)+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{x}^{{k}} }{{k}.{k}!} \\ $$$$\int\frac{{e}^{{x}} {ln}\left({x}\right)}{{x}}{dx}={Ei}\left({x}\right){ln}\left({x}\right)−\int\frac{\mathrm{1}}{{x}}\left(\gamma+{ln}\left({x}\right)+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{x}^{{k}} }{{k}.{k}!}\right){dx} \\ $$$$={Ei}\left({x}\right){ln}\left({x}\right)−\int\frac{\gamma}{{x}}{dx}−\int\frac{{ln}\left({x}\right)}{{x}}{dx}−\underset{{k}\geqslant\mathrm{1}} {\sum}\int\frac{{x}^{{k}−\mathrm{1}} }{{k}.{k}!}{dx} \\ $$$$={Ei}\left({x}\right){ln}\left({x}\right)−\gamma{ln}\left({x}\right)−\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}}−\underset{{k}\geqslant\mathrm{0}} {\sum}\int\frac{{x}^{{k}} }{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{1}\right)!}{dx} \\ $$$$={Ei}\left({x}\right){ln}\left({x}\right)−\gamma{ln}\left({x}\right)−\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}}−\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}+\mathrm{1}} }{\left({k}+\mathrm{1}\right)^{\mathrm{2}} \left({k}+\mathrm{1}\right)!}+{c} \\ $$$$\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}+\mathrm{1}} }{\left({k}+\mathrm{1}\right)^{\mathrm{2}} \left({k}+\mathrm{1}\right)!}=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{k}!.{k}!.{k}!}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} \left({k}+\mathrm{1}\right)!.{k}!.{k}!}.\frac{{x}^{{k}+\mathrm{1}} }{{k}!} \\ $$$$={x}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{k}!.{k}!.{k}!}{\left({k}+\mathrm{1}\right)!\left({k}+\mathrm{1}\right)!\left({k}+\mathrm{1}\right)!}\frac{{x}^{{k}} }{{k}!} \\ $$$${k}!=\left(\mathrm{1}\right)_{{k}} ,\left({k}+\mathrm{1}\right)!=\left(\mathrm{2}\right)_{{k}} \\ $$$$={x}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(\mathrm{1}\right)_{{k}} \left(\mathrm{1}\right)_{{k}} \left(\mathrm{1}\right)_{{k}} }{\left(\mathrm{2}\right)_{{k}} \left(\mathrm{2}\right)_{{k}} \left(\mathrm{2}\right)_{{k}} }.\frac{{x}^{{k}} }{{k}!}={x}_{\mathrm{3}} {F}_{\mathrm{3}} \left(\mathrm{1},\mathrm{1},\mathrm{1};\mathrm{2},\mathrm{2},\mathrm{2};{x}\right) \\ $$$${we}\:{Get} \\ $$$$\int\frac{{e}^{{x}} {ln}\left({x}\right)}{{x}}{dx}={E}_{{i}} \left({x}\right){ln}\left({x}\right)−\gamma{ln}\left({x}\right)−\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}}−{x}\:_{\mathrm{3}} {F}_{\mathrm{3}} \left(\mathrm{1},\mathrm{1},\mathrm{1};\mathrm{2},\mathrm{2},\mathrm{2};{x}\right)+{c} \\ $$$$=\frac{{ln}\left({x}\right)}{\mathrm{2}}\left({Ei}\left({x}\right)−\mathrm{2}\gamma+{ln}\left(\frac{\mathrm{1}}{{x}}\right)\right)−{x}\:_{\mathrm{3}} {F}_{\mathrm{3}} \left(\mathrm{1},\mathrm{1},\mathrm{1};\mathrm{2},\mathrm{2},\mathrm{2};{x}\right)+{c} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply