Question Number 116466 by mr W last updated on 04/Oct/20

Commented by mr W last updated on 04/Oct/20
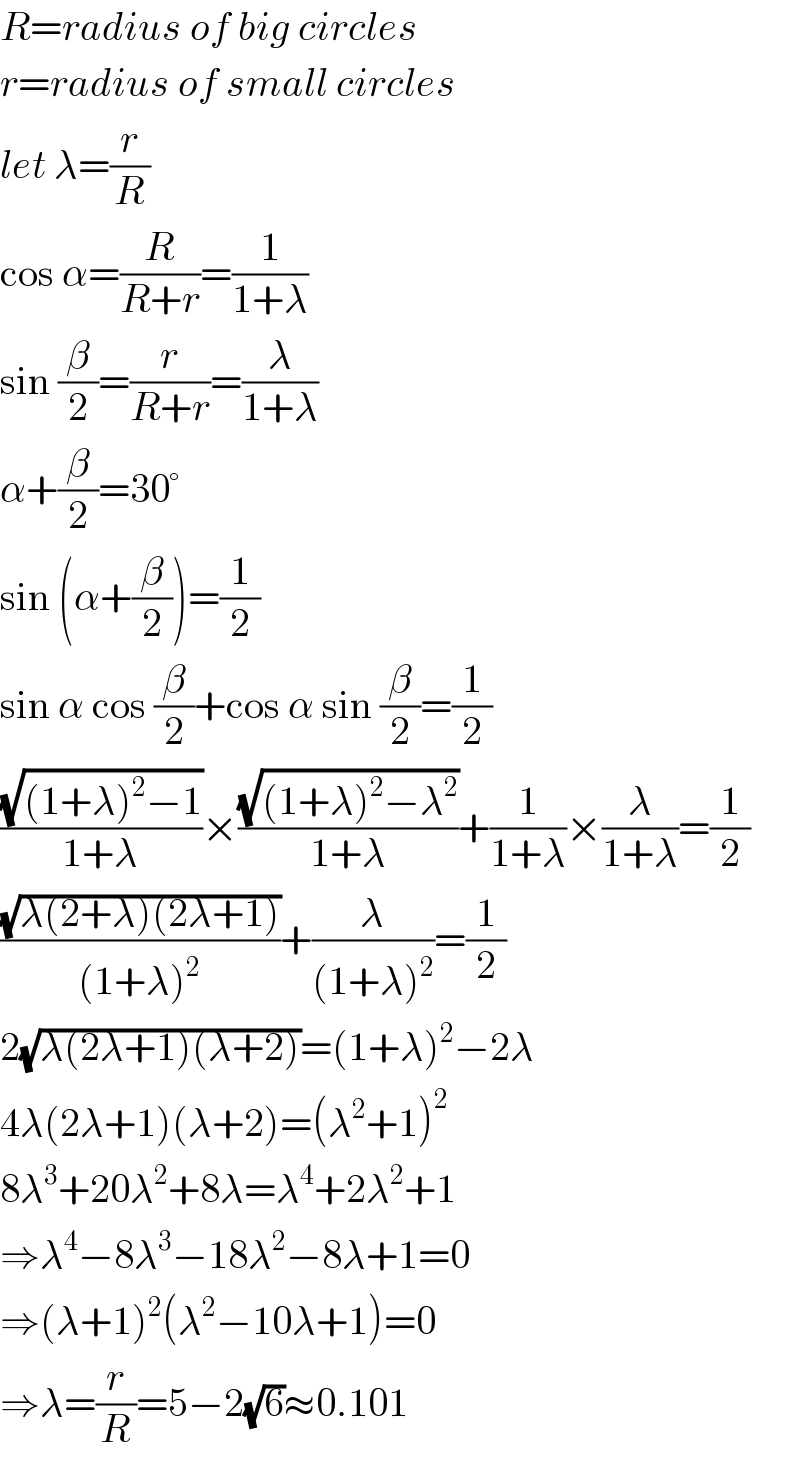
$${R}={radius}\:{of}\:{big}\:{circles} \\ $$$${r}={radius}\:{of}\:{small}\:{circles} \\ $$$${let}\:\lambda=\frac{{r}}{{R}} \\ $$$$\mathrm{cos}\:\alpha=\frac{{R}}{{R}+{r}}=\frac{\mathrm{1}}{\mathrm{1}+\lambda} \\ $$$$\mathrm{sin}\:\frac{\beta}{\mathrm{2}}=\frac{{r}}{{R}+{r}}=\frac{\lambda}{\mathrm{1}+\lambda} \\ $$$$\alpha+\frac{\beta}{\mathrm{2}}=\mathrm{30}° \\ $$$$\mathrm{sin}\:\left(\alpha+\frac{\beta}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\alpha\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}+\mathrm{cos}\:\alpha\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\sqrt{\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} −\mathrm{1}}}{\mathrm{1}+\lambda}×\frac{\sqrt{\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} −\lambda^{\mathrm{2}} }}{\mathrm{1}+\lambda}+\frac{\mathrm{1}}{\mathrm{1}+\lambda}×\frac{\lambda}{\mathrm{1}+\lambda}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\sqrt{\lambda\left(\mathrm{2}+\lambda\right)\left(\mathrm{2}\lambda+\mathrm{1}\right)}}{\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} }+\frac{\lambda}{\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}\sqrt{\lambda\left(\mathrm{2}\lambda+\mathrm{1}\right)\left(\lambda+\mathrm{2}\right)}=\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} −\mathrm{2}\lambda \\ $$$$\mathrm{4}\lambda\left(\mathrm{2}\lambda+\mathrm{1}\right)\left(\lambda+\mathrm{2}\right)=\left(\lambda^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{8}\lambda^{\mathrm{3}} +\mathrm{20}\lambda^{\mathrm{2}} +\mathrm{8}\lambda=\lambda^{\mathrm{4}} +\mathrm{2}\lambda^{\mathrm{2}} +\mathrm{1} \\ $$$$\Rightarrow\lambda^{\mathrm{4}} −\mathrm{8}\lambda^{\mathrm{3}} −\mathrm{18}\lambda^{\mathrm{2}} −\mathrm{8}\lambda+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\lambda+\mathrm{1}\right)^{\mathrm{2}} \left(\lambda^{\mathrm{2}} −\mathrm{10}\lambda+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{{r}}{{R}}=\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\approx\mathrm{0}.\mathrm{101} \\ $$
Commented by I want to learn more last updated on 04/Oct/20
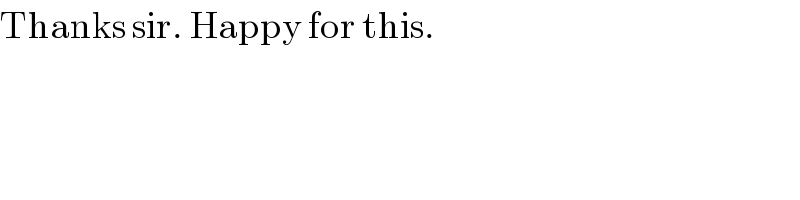
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{Happy}\:\mathrm{for}\:\mathrm{this}. \\ $$
Commented by I want to learn more last updated on 04/Oct/20
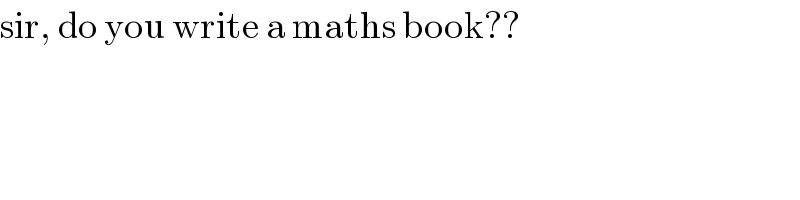
$$\mathrm{sir},\:\mathrm{do}\:\mathrm{you}\:\mathrm{write}\:\mathrm{a}\:\mathrm{maths}\:\mathrm{book}?? \\ $$
Commented by mr W last updated on 04/Oct/20

$${no} \\ $$
Commented by I want to learn more last updated on 04/Oct/20

$$\mathrm{Okay}\:\mathrm{sir} \\ $$
