Question Number 116486 by ZiYangLee last updated on 04/Oct/20
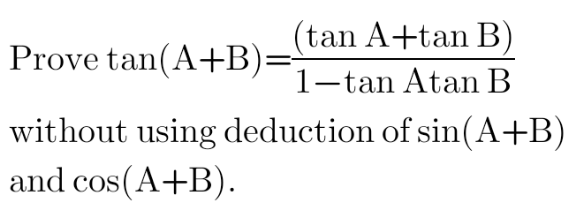
Answered by Dwaipayan Shikari last updated on 04/Oct/20
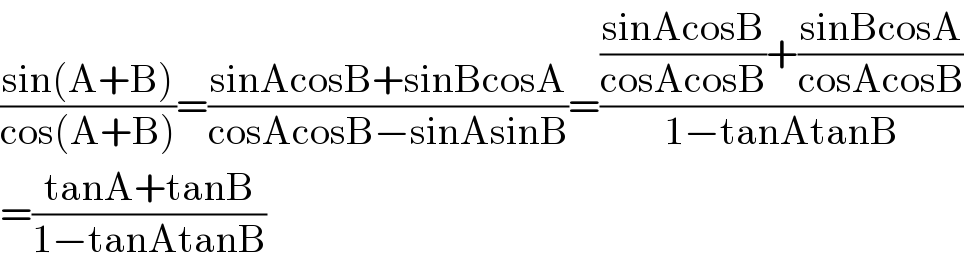
$$\frac{\mathrm{sin}\left(\mathrm{A}+\mathrm{B}\right)}{\mathrm{cos}\left(\mathrm{A}+\mathrm{B}\right)}=\frac{\mathrm{sinAcosB}+\mathrm{sinBcosA}}{\mathrm{cosAcosB}−\mathrm{sinAsinB}}=\frac{\frac{\mathrm{sinAcosB}}{\mathrm{cosAcosB}}+\frac{\mathrm{sinBcosA}}{\mathrm{cosAcosB}}}{\mathrm{1}−\mathrm{tanAtanB}} \\ $$$$=\frac{\mathrm{tanA}+\mathrm{tanB}}{\mathrm{1}−\mathrm{tanAtanB}} \\ $$
Answered by Olaf last updated on 04/Oct/20

$${x}\:=\:\mathrm{tan}\left({a}+{b}\right)\left(\mathrm{1}−\mathrm{tan}{a}\mathrm{tan}{b}\right)\:\left(\mathrm{1}\right) \\ $$$${x}\:=\:\frac{\mathrm{sin}\left({a}+{b}\right)}{\mathrm{cos}\left({a}+{b}\right)}\left(\mathrm{1}−\frac{\mathrm{sin}{a}\mathrm{sin}{b}}{\mathrm{cos}{a}\mathrm{cos}{b}}\right) \\ $$$$ \\ $$$${x}\:=\:\frac{\frac{{e}^{{i}\left({a}+{b}\right)} −{e}^{−{i}\left({a}+{b}\right)} }{\mathrm{2}{i}}}{\frac{{e}^{{i}\left({a}+{b}\right)} +{e}^{−{i}\left({a}+{b}\right)} }{\mathrm{2}}}\left(\mathrm{1}−\frac{\frac{{e}^{{ia}} −{e}^{−{ia}} }{\mathrm{2}{i}}.\frac{{e}^{{ib}} −{e}^{−{ib}} }{\mathrm{2}{i}}}{\frac{{e}^{{ia}} +{e}^{−{ia}} }{\mathrm{2}}.\frac{{e}^{{ib}} +{e}^{{ib}} }{\mathrm{2}}}\right) \\ $$$${x}\:=\:−{i}\frac{{e}^{{i}\left({a}+{b}\right)} −{e}^{−{i}\left({a}+{b}\right)} }{{e}^{{i}\left({a}+{b}\right)} +{e}^{{i}\left({a}+{b}\right)} }\left(\mathrm{1}+\frac{\left({e}^{{ia}} −{e}^{−{ia}} \right)\left({e}^{{ib}} −{e}^{−{ib}} \right)}{\left({e}^{{ia}} +{e}^{{ia}} \right)\left({e}^{{ib}} +{e}^{−{ib}} \right)}\right) \\ $$$$\mathrm{After}\:\mathrm{simplification}\:: \\ $$$${x}\:=\:−{i}\frac{{e}^{{ia}} −{e}^{−{ia}} }{{e}^{{ia}} +{e}^{{ia}} }−{i}\frac{{e}^{{ib}} −{e}^{−{ib}} }{{e}^{{ib}} +{e}^{{ib}} } \\ $$$${x}\:=\:\frac{\frac{{e}^{{ia}} −{e}^{−{ia}} }{\mathrm{2}{i}}}{\frac{{e}^{{ia}} +{e}^{−{ia}} }{\mathrm{2}}}+\frac{\frac{{e}^{{ib}} −{e}^{−{ib}} }{\mathrm{2}{i}}}{\frac{{e}^{{ib}} +{e}^{−{ib}} }{\mathrm{2}}} \\ $$$${x}\:=\:\frac{\mathrm{sin}{a}}{\mathrm{cos}{a}}+\frac{\mathrm{sin}{b}}{\mathrm{cos}{b}} \\ $$$${x}\:=\:\mathrm{tan}{a}+\mathrm{tan}{b}\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:: \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{tan}\left({a}+{b}\right)\left(\mathrm{1}−\mathrm{tan}{a}\mathrm{tan}{b}\right)\:=\:\mathrm{tan}{a}+\mathrm{tan}{b} \\ $$
Commented by ZiYangLee last updated on 05/Oct/20

$$\bigstar \\ $$
