Question Number 116523 by zakirullah last updated on 04/Oct/20

Answered by Olaf last updated on 04/Oct/20
![(1+a) determinant (((1+b),1),(1,(1+c)))− determinant ((1,1),(1,(1+c)))+ determinant ((1,1),((1+b),1)) = (1+a)[(1+b)(1+c)−1] −(1+c−1)+(1−1−b) = (1+a)(b+c+bc)−c−b = b+c+bc+ab+ac+abc−c−b = abc+bc+ac+ab = abc(1+(1/a)+(1/b)+(1/c))](https://www.tinkutara.com/question/Q116525.png)
$$\left(\mathrm{1}+{a}\right)\begin{vmatrix}{\mathrm{1}+{b}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}+{c}}\end{vmatrix}−\begin{vmatrix}{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}+{c}}\end{vmatrix}+\begin{vmatrix}{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}+{b}}&{\mathrm{1}}\end{vmatrix} \\ $$$$ \\ $$$$=\:\left(\mathrm{1}+{a}\right)\left[\left(\mathrm{1}+{b}\right)\left(\mathrm{1}+{c}\right)−\mathrm{1}\right] \\ $$$$−\left(\mathrm{1}+{c}−\mathrm{1}\right)+\left(\mathrm{1}−\mathrm{1}−{b}\right) \\ $$$$ \\ $$$$=\:\left(\mathrm{1}+{a}\right)\left({b}+{c}+{bc}\right)−{c}−{b} \\ $$$$=\:{b}+{c}+{bc}+{ab}+{ac}+{abc}−{c}−{b} \\ $$$$=\:{abc}+{bc}+{ac}+{ab} \\ $$$$=\:{abc}\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right) \\ $$
Commented by zakirullah last updated on 04/Oct/20

$$\:\:\:\:\:\:\:{thank}\:{you}\:{sir} \\ $$
Answered by $@y@m last updated on 04/Oct/20
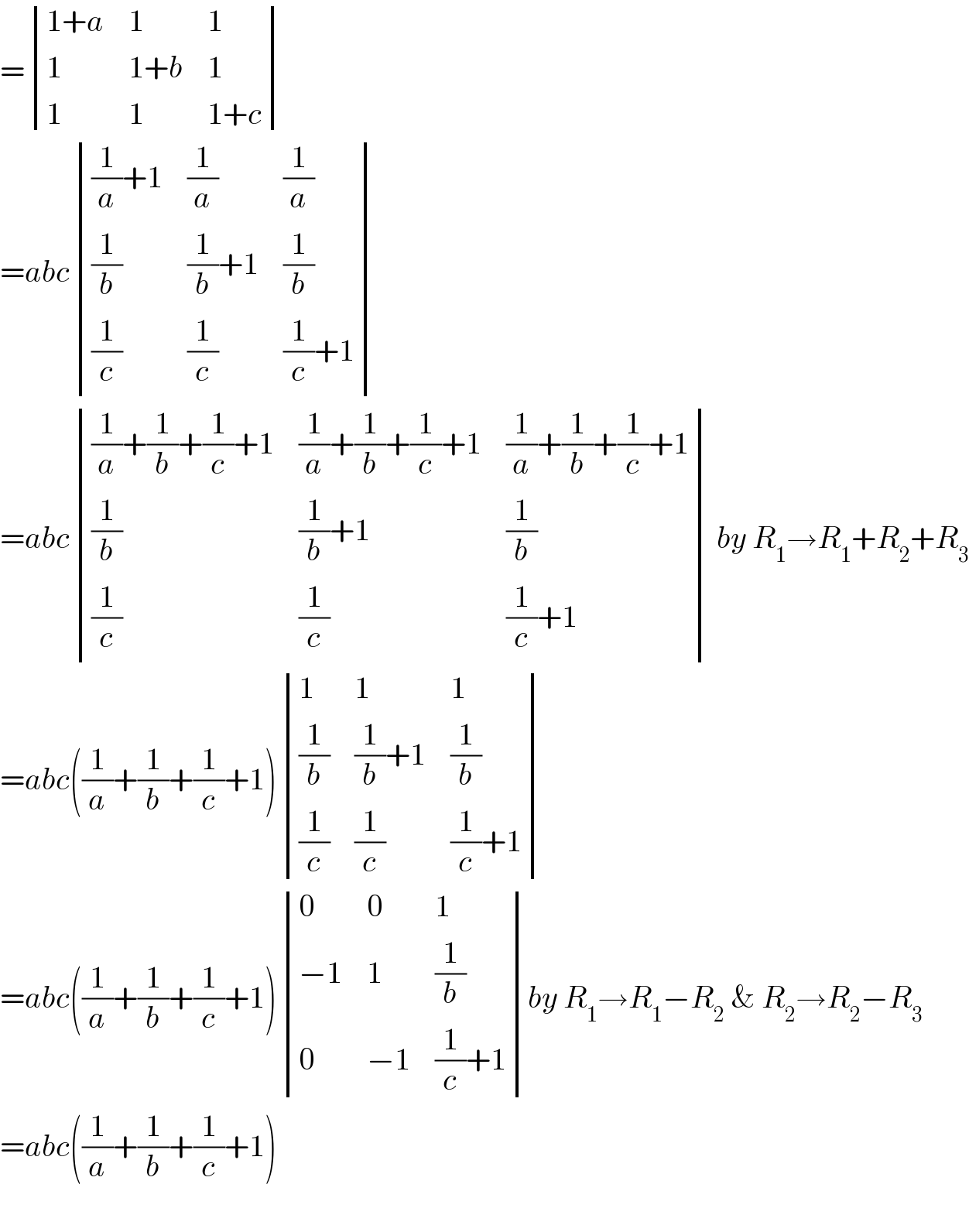
$$=\begin{vmatrix}{\mathrm{1}+{a}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}+{b}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}+{c}}\end{vmatrix} \\ $$$$={abc}\begin{vmatrix}{\frac{\mathrm{1}}{{a}}+\mathrm{1}}&{\frac{\mathrm{1}}{{a}}}&{\frac{\mathrm{1}}{{a}}}\\{\frac{\mathrm{1}}{{b}}}&{\frac{\mathrm{1}}{{b}}+\mathrm{1}}&{\frac{\mathrm{1}}{{b}}}\\{\frac{\mathrm{1}}{{c}}}&{\frac{\mathrm{1}}{{c}}}&{\frac{\mathrm{1}}{{c}}+\mathrm{1}}\end{vmatrix} \\ $$$$={abc}\begin{vmatrix}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\mathrm{1}}&{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\mathrm{1}}&{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\mathrm{1}}\\{\frac{\mathrm{1}}{{b}}}&{\frac{\mathrm{1}}{{b}}+\mathrm{1}}&{\frac{\mathrm{1}}{{b}}}\\{\frac{\mathrm{1}}{{c}}}&{\frac{\mathrm{1}}{{c}}}&{\frac{\mathrm{1}}{{c}}+\mathrm{1}}\end{vmatrix}\:{by}\:{R}_{\mathrm{1}} \rightarrow{R}_{\mathrm{1}} +{R}_{\mathrm{2}} +{R}_{\mathrm{3}} \\ $$$$={abc}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\mathrm{1}\right)\begin{vmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}\\{\frac{\mathrm{1}}{{b}}}&{\frac{\mathrm{1}}{{b}}+\mathrm{1}}&{\frac{\mathrm{1}}{{b}}}\\{\frac{\mathrm{1}}{{c}}}&{\frac{\mathrm{1}}{{c}}}&{\frac{\mathrm{1}}{{c}}+\mathrm{1}}\end{vmatrix} \\ $$$$={abc}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\mathrm{1}\right)\begin{vmatrix}{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\\{−\mathrm{1}}&{\mathrm{1}}&{\frac{\mathrm{1}}{{b}}}\\{\mathrm{0}}&{−\mathrm{1}}&{\frac{\mathrm{1}}{{c}}+\mathrm{1}}\end{vmatrix}{by}\:{R}_{\mathrm{1}} \rightarrow{R}_{\mathrm{1}} −{R}_{\mathrm{2}} \:\&\:{R}_{\mathrm{2}} \rightarrow{R}_{\mathrm{2}} −{R}_{\mathrm{3}} \\ $$$$={abc}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\mathrm{1}\right) \\ $$$$ \\ $$
Commented by zakirullah last updated on 04/Oct/20

$$\:\:\:\:\:\:\:\mathrm{thanks}\:\mathrm{alot} \\ $$
