Question Number 116674 by ZiYangLee last updated on 05/Oct/20
Commented by ZiYangLee last updated on 05/Oct/20

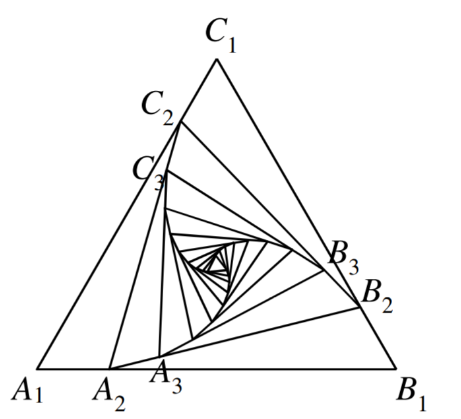
$${A}_{\mathrm{1}} {B}_{\mathrm{1}} {C}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{regular}\:\mathrm{triangle}. \\ $$$${A}_{\mathrm{2}} {B}_{\mathrm{2}} {C}_{\mathrm{2}} \mathrm{are}\:\mathrm{points}\:\mathrm{on}\:{A}_{\mathrm{1}} {B}_{\mathrm{1}} ,{A}_{\mathrm{2}} {B}_{\mathrm{2}} ,{C}_{\mathrm{1}} {A}_{\mathrm{1}} \: \\ $$$$\mathrm{respectively}\:\mathrm{such}\:\mathrm{that}\:{A}_{\mathrm{1}} {A}_{\mathrm{2}} ={B}_{\mathrm{1}} {B}_{\mathrm{2}} ={C}_{\mathrm{1}} {C}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{5}}{A}_{\mathrm{1}} {B}_{\mathrm{1}} . \\ $$$${A}_{\mathrm{3}} {B}_{\mathrm{3}} {C}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{points}\:\mathrm{on}\:{A}_{\mathrm{2}} {B}_{\mathrm{2}} ,{B}_{\mathrm{2}} {C}_{\mathrm{2}} ,{C}_{\mathrm{2}} {A}_{\mathrm{2}} \\ $$$$\mathrm{respectively}\:\mathrm{such}\:\mathrm{that}\:{A}_{\mathrm{2}} {A}_{\mathrm{3}} ={B}_{\mathrm{2}} {B}_{\mathrm{3}} ={C}_{\mathrm{2}} {C}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{5}}{A}_{\mathrm{2}} {A}_{\mathrm{3}} \\ $$$$\mathrm{Repeat}\:\mathrm{this}\:\mathrm{process}\:\mathrm{to}\:\mathrm{constract}\:\mathrm{infinitely} \\ $$$$\mathrm{many}\:\mathrm{triangles}\:\bigtriangleup{A}_{\mathrm{1}} {B}_{\mathrm{1}} {C}_{\mathrm{1}} ,\bigtriangleup{A}_{\mathrm{2}} {B}_{\mathrm{2}} {C}_{\mathrm{2}} ,\bigtriangleup{A}_{\mathrm{3}} {B}_{\mathrm{3}} {C}_{\mathrm{3}} ,\ldots \\ $$$$\mathrm{If}\:{S}_{{n}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\bigtriangleup{A}_{{n}} {B}_{{n}} {C}_{{n}} , \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\frac{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{S}_{{n}} }{{S}_{\mathrm{1}} }=\frac{{S}_{\mathrm{1}} +{S}_{\mathrm{2}} +{S}_{\mathrm{3}} +\ldots}{{S}_{\mathrm{1}} } \\ $$
Answered by mr W last updated on 05/Oct/20
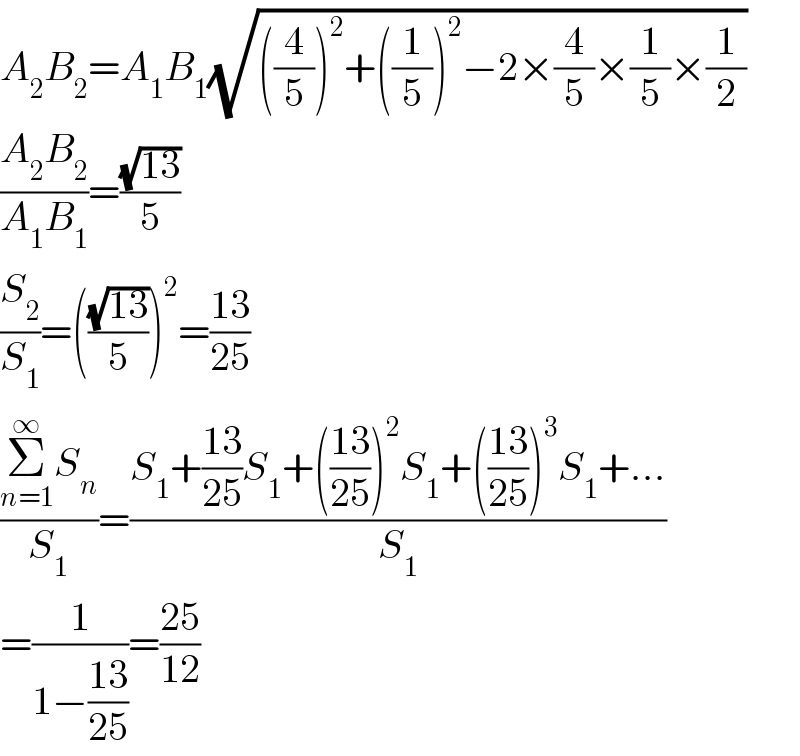
$${A}_{\mathrm{2}} {B}_{\mathrm{2}} ={A}_{\mathrm{1}} {B}_{\mathrm{1}} \sqrt{\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} −\mathrm{2}×\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\frac{{A}_{\mathrm{2}} {B}_{\mathrm{2}} }{{A}_{\mathrm{1}} {B}_{\mathrm{1}} }=\frac{\sqrt{\mathrm{13}}}{\mathrm{5}} \\ $$$$\frac{{S}_{\mathrm{2}} }{{S}_{\mathrm{1}} }=\left(\frac{\sqrt{\mathrm{13}}}{\mathrm{5}}\right)^{\mathrm{2}} =\frac{\mathrm{13}}{\mathrm{25}} \\ $$$$\frac{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{S}_{{n}} }{{S}_{\mathrm{1}} }=\frac{{S}_{\mathrm{1}} +\frac{\mathrm{13}}{\mathrm{25}}{S}_{\mathrm{1}} +\left(\frac{\mathrm{13}}{\mathrm{25}}\right)^{\mathrm{2}} {S}_{\mathrm{1}} +\left(\frac{\mathrm{13}}{\mathrm{25}}\right)^{\mathrm{3}} {S}_{\mathrm{1}} +…}{{S}_{\mathrm{1}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{13}}{\mathrm{25}}}=\frac{\mathrm{25}}{\mathrm{12}} \\ $$
Commented by ZiYangLee last updated on 06/Oct/20

$$\mathrm{Finally}…\mathrm{This}\:\mathrm{morning}\:\mathrm{my}\:\mathrm{Tinkutara}\:\mathrm{had}\:\mathrm{a}\: \\ $$$$\mathrm{trouble}\:\mathrm{that}\:\mathrm{it}\:\mathrm{couldnt}\:\mathrm{load}\:\mathrm{for}\:\mathrm{the}\:\mathrm{Forum} \\ $$
Answered by Olaf last updated on 05/Oct/20
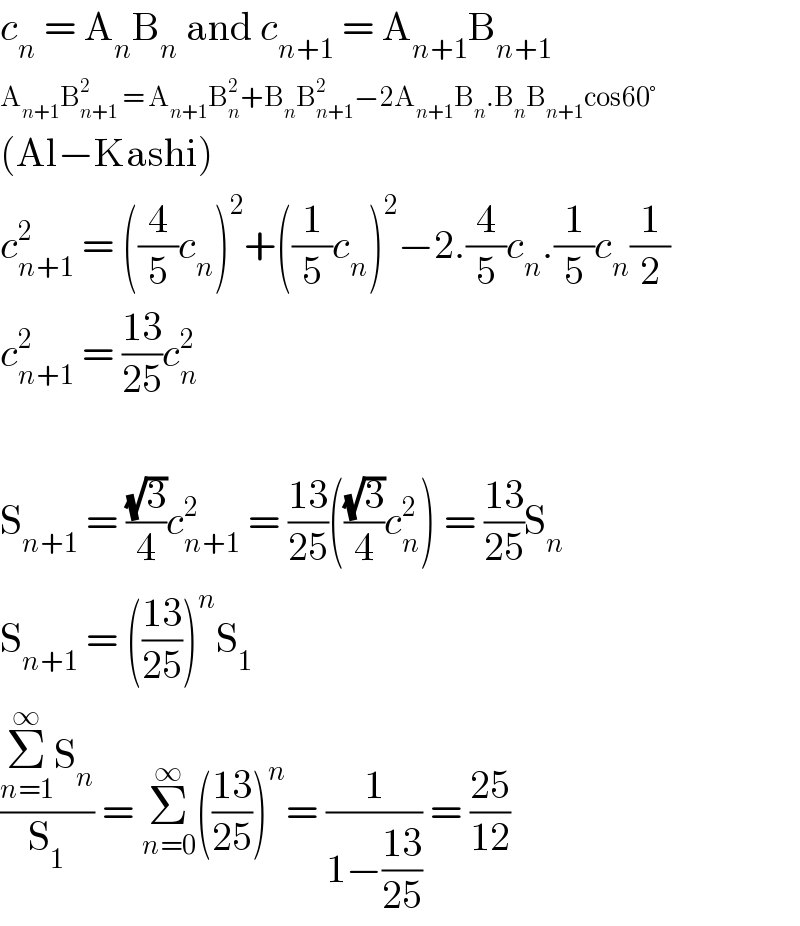
$${c}_{{n}} \:=\:\mathrm{A}_{{n}} \mathrm{B}_{{n}} \:\mathrm{and}\:{c}_{{n}+\mathrm{1}} \:=\:\mathrm{A}_{{n}+\mathrm{1}} \mathrm{B}_{{n}+\mathrm{1}} \\ $$$$\mathrm{A}_{{n}+\mathrm{1}} \mathrm{B}_{{n}+\mathrm{1}} ^{\mathrm{2}} \:=\:\mathrm{A}_{{n}+\mathrm{1}} \mathrm{B}_{{n}} ^{\mathrm{2}} +\mathrm{B}_{{n}} \mathrm{B}_{{n}+\mathrm{1}} ^{\mathrm{2}} −\mathrm{2A}_{{n}+\mathrm{1}} \mathrm{B}_{{n}} .\mathrm{B}_{{n}} \mathrm{B}_{{n}+\mathrm{1}} \mathrm{cos60}° \\ $$$$\left(\mathrm{Al}−\mathrm{Kashi}\right) \\ $$$${c}_{{n}+\mathrm{1}} ^{\mathrm{2}} \:=\:\left(\frac{\mathrm{4}}{\mathrm{5}}{c}_{{n}} \right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{5}}{c}_{{n}} \right)^{\mathrm{2}} −\mathrm{2}.\frac{\mathrm{4}}{\mathrm{5}}{c}_{{n}} .\frac{\mathrm{1}}{\mathrm{5}}{c}_{{n}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$${c}_{{n}+\mathrm{1}} ^{\mathrm{2}} \:=\:\frac{\mathrm{13}}{\mathrm{25}}{c}_{{n}} ^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{S}_{{n}+\mathrm{1}} \:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{c}_{{n}+\mathrm{1}} ^{\mathrm{2}} \:=\:\frac{\mathrm{13}}{\mathrm{25}}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{c}_{{n}} ^{\mathrm{2}} \right)\:=\:\frac{\mathrm{13}}{\mathrm{25}}\mathrm{S}_{{n}} \\ $$$$\mathrm{S}_{{n}+\mathrm{1}} \:=\:\left(\frac{\mathrm{13}}{\mathrm{25}}\right)^{{n}} \mathrm{S}_{\mathrm{1}} \\ $$$$\frac{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{S}_{{n}} }{\mathrm{S}_{\mathrm{1}} }\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{13}}{\mathrm{25}}\right)^{{n}} =\:\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{13}}{\mathrm{25}}}\:=\:\frac{\mathrm{25}}{\mathrm{12}} \\ $$
