Question Number 116759 by bemath last updated on 06/Oct/20

Answered by bobhans last updated on 06/Oct/20
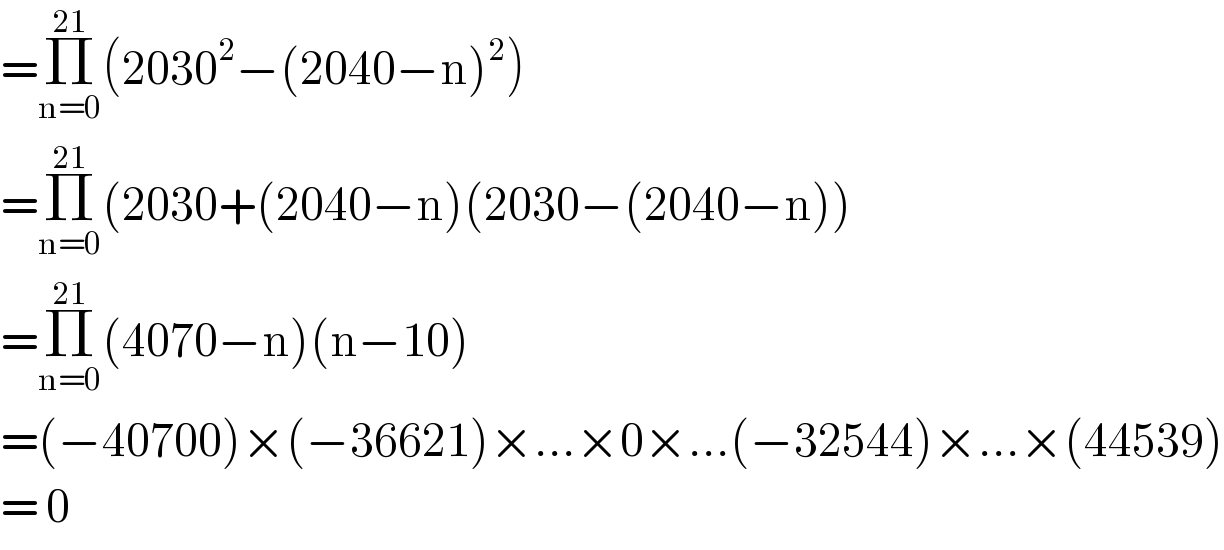
$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\mathrm{21}} {\prod}}\left(\mathrm{2030}^{\mathrm{2}} −\left(\mathrm{2040}−\mathrm{n}\right)^{\mathrm{2}} \right) \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\mathrm{21}} {\prod}}\left(\mathrm{2030}+\left(\mathrm{2040}−\mathrm{n}\right)\left(\mathrm{2030}−\left(\mathrm{2040}−\mathrm{n}\right)\right)\right. \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\mathrm{21}} {\prod}}\left(\mathrm{4070}−\mathrm{n}\right)\left(\mathrm{n}−\mathrm{10}\right) \\ $$$$=\left(−\mathrm{40700}\right)×\left(−\mathrm{36621}\right)×…×\mathrm{0}×…\left(−\mathrm{32544}\right)×…×\left(\mathrm{44539}\right) \\ $$$$=\:\mathrm{0} \\ $$
Answered by Dwaipayan Shikari last updated on 06/Oct/20
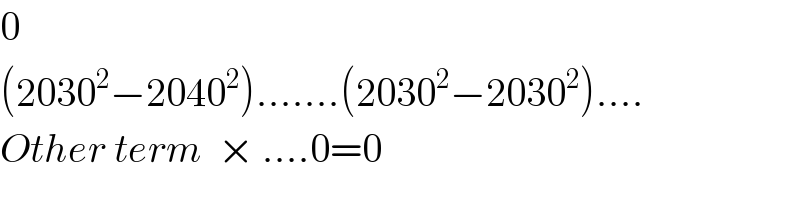
$$\mathrm{0} \\ $$$$\left(\mathrm{2030}^{\mathrm{2}} −\mathrm{2040}^{\mathrm{2}} \right)…….\left(\mathrm{2030}^{\mathrm{2}} −\mathrm{2030}^{\mathrm{2}} \right)…. \\ $$$${Other}\:{term}\:\:×\:….\mathrm{0}=\mathrm{0} \\ $$
