Question Number 116780 by ajfour last updated on 06/Oct/20

Commented by ajfour last updated on 06/Oct/20
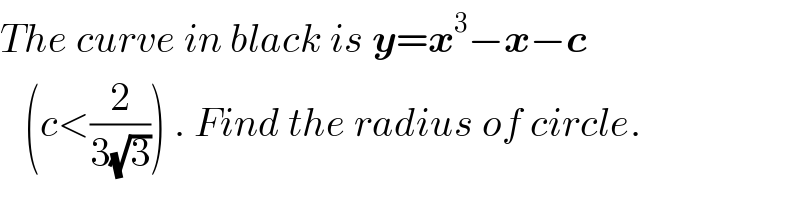
$${The}\:{curve}\:{in}\:{black}\:{is}\:\boldsymbol{{y}}=\boldsymbol{{x}}^{\mathrm{3}} −\boldsymbol{{x}}−\boldsymbol{{c}} \\ $$$$\:\:\:\left({c}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)\:.\:{Find}\:{the}\:{radius}\:{of}\:{circle}. \\ $$
Answered by mr W last updated on 07/Oct/20
![x^3 −x−c=0 ⇒x=((2(√3))/3)sin (−(1/3)sin^(−1) ((3(√3)c)/2)+((2kπ)/3)) α=−((2(√3))/3)sin ((π/3)−(1/3)sin^(−1) ((3(√3)c)/2)) β=−((2(√3))/3)sin ((1/3)sin^(−1) ((3(√3)c)/2)) r=−((α+β)/2) =((√3)/3)[sin ((1/3)sin^(−1) ((3(√3)c)/2))+sin ((π/3)−(1/3)sin^(−1) ((3(√3)c)/2))] =((√3)/3)[sin ((1/3)sin^(−1) ((3(√3)c)/2))+sin (π/3)cos ((1/3)sin^(−1) ((3(√3)c)/2))−cos (π/3) sin ((1/3)sin^(−1) ((3(√3)c)/2))] =((√3)/3)sin (1/3)(π+sin^(−1) ((3(√3)c)/2))](https://www.tinkutara.com/question/Q116791.png)
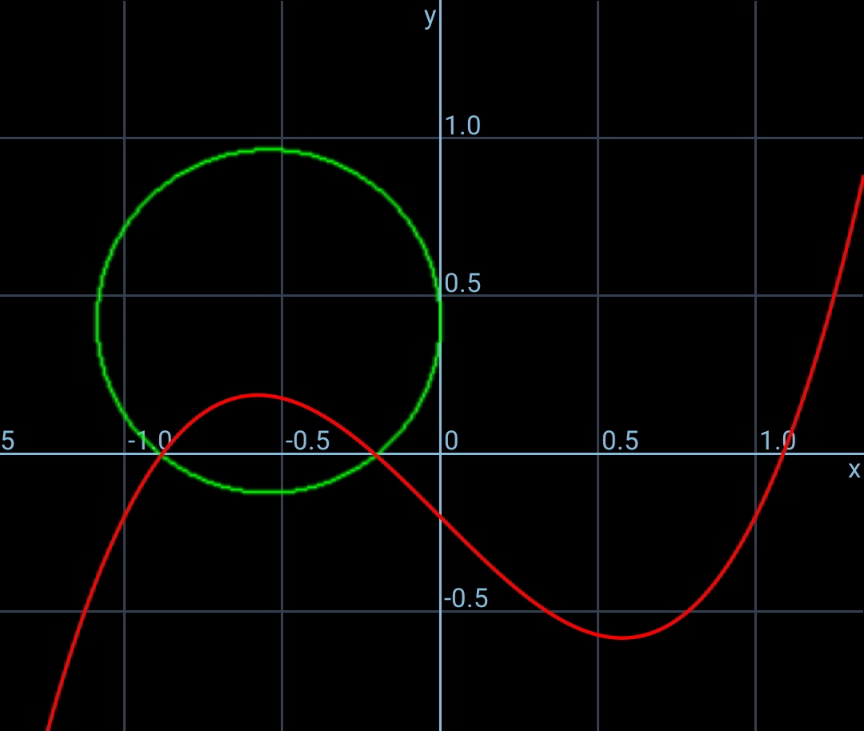
$${x}^{\mathrm{3}} −{x}−{c}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right) \\ $$$$ \\ $$$$\alpha=−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}\right) \\ $$$$\beta=−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}\right) \\ $$$${r}=−\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}\right)+\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}\right)\right] \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}\right)+\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}\right)−\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}\right)\right] \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{3}}\left(\pi+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}\right) \\ $$
Commented by mr W last updated on 06/Oct/20
Answered by ajfour last updated on 13/Oct/20
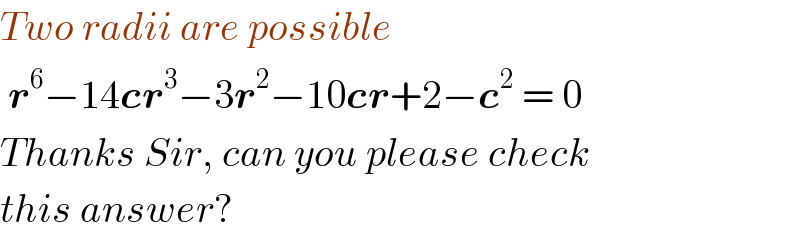
$${Two}\:{radii}\:{are}\:{possible} \\ $$$$\:\boldsymbol{{r}}^{\mathrm{6}} −\mathrm{14}\boldsymbol{{cr}}^{\mathrm{3}} −\mathrm{3}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{{cr}}+\mathrm{2}−\boldsymbol{{c}}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$${Thanks}\:{Sir},\:{can}\:{you}\:{please}\:{check} \\ $$$${this}\:{answer}? \\ $$
Commented by mr W last updated on 13/Oct/20
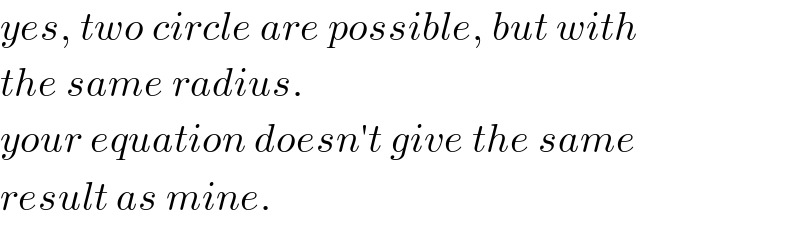
$${yes},\:{two}\:{circle}\:{are}\:{possible},\:{but}\:{with} \\ $$$${the}\:{same}\:{radius}. \\ $$$${your}\:{equation}\:{doesn}'{t}\:{give}\:{the}\:{same} \\ $$$${result}\:{as}\:{mine}. \\ $$
Commented by ajfour last updated on 13/Oct/20
$${sorry}\:{sir},\:{i}\:{had}\:{another}\:{circle} \\ $$$${in}\:{my}\:{thoughts},\:{See}\:{Q}.\:\mathrm{117827}.. \\ $$
