Question Number 116800 by mr W last updated on 06/Oct/20

Answered by bobhans last updated on 07/Oct/20
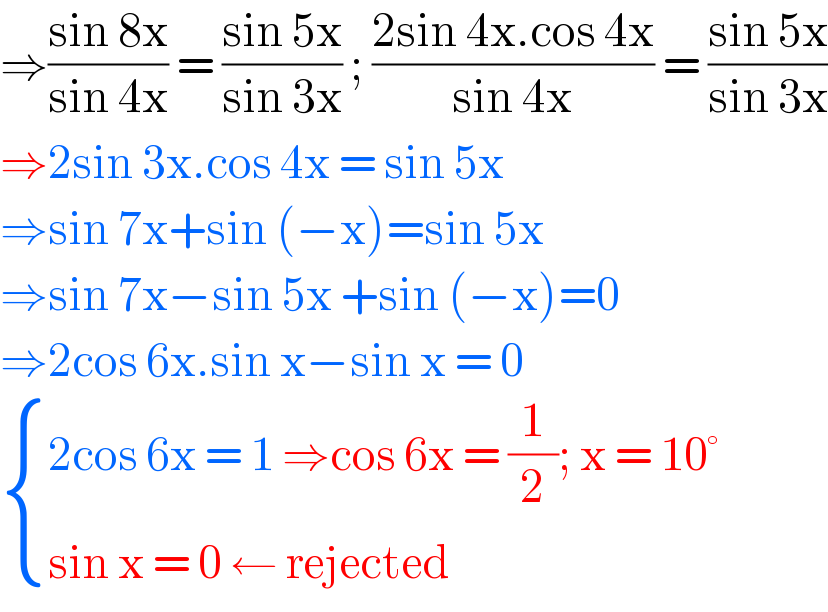
$$\Rightarrow\frac{\mathrm{sin}\:\mathrm{8x}}{\mathrm{sin}\:\mathrm{4x}}\:=\:\frac{\mathrm{sin}\:\mathrm{5x}}{\mathrm{sin}\:\mathrm{3x}}\:;\:\frac{\mathrm{2sin}\:\mathrm{4x}.\mathrm{cos}\:\mathrm{4x}}{\mathrm{sin}\:\mathrm{4x}}\:=\:\frac{\mathrm{sin}\:\mathrm{5x}}{\mathrm{sin}\:\mathrm{3x}} \\ $$$$\Rightarrow\mathrm{2sin}\:\mathrm{3x}.\mathrm{cos}\:\mathrm{4x}\:=\:\mathrm{sin}\:\mathrm{5x} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{7x}+\mathrm{sin}\:\left(−\mathrm{x}\right)=\mathrm{sin}\:\mathrm{5x} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{7x}−\mathrm{sin}\:\mathrm{5x}\:+\mathrm{sin}\:\left(−\mathrm{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2cos}\:\mathrm{6x}.\mathrm{sin}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{0} \\ $$$$\begin{cases}{\mathrm{2cos}\:\mathrm{6x}\:=\:\mathrm{1}\:\Rightarrow\mathrm{cos}\:\mathrm{6x}\:=\:\frac{\mathrm{1}}{\mathrm{2}};\:\mathrm{x}\:=\:\mathrm{10}°}\\{\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{0}\:\leftarrow\:\mathrm{rejected}}\end{cases} \\ $$
Commented by mr W last updated on 07/Oct/20

$${nice}! \\ $$
