Question Number 116845 by mohammad17 last updated on 07/Oct/20

Commented by mohammad17 last updated on 07/Oct/20

$${help}\:{me}\:{sir}\: \\ $$
Answered by TANMAY PANACEA last updated on 07/Oct/20
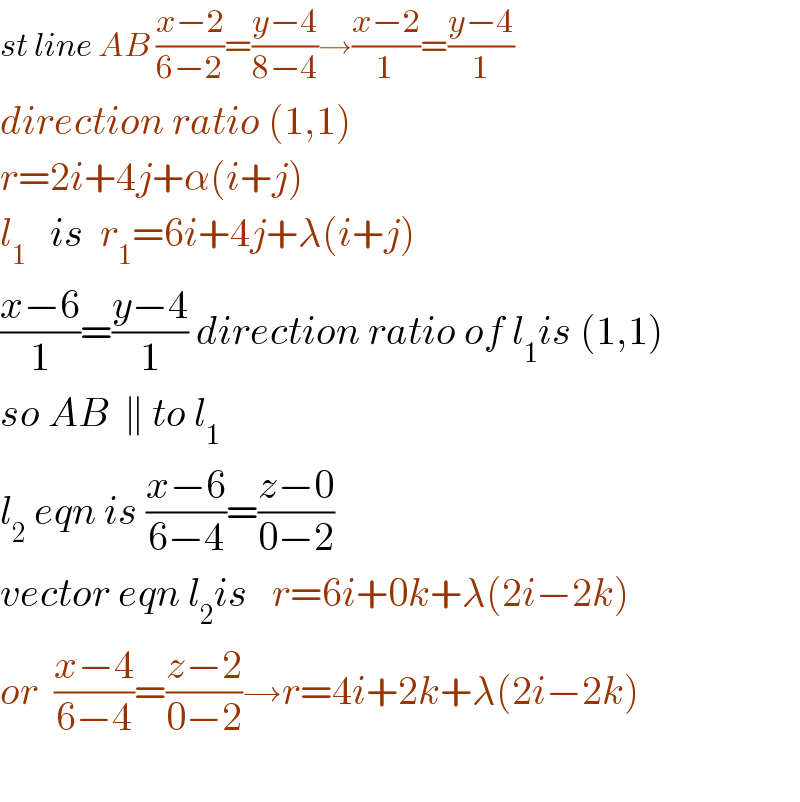
$${st}\:{line}\:{AB}\:\frac{{x}−\mathrm{2}}{\mathrm{6}−\mathrm{2}}=\frac{{y}−\mathrm{4}}{\mathrm{8}−\mathrm{4}}\rightarrow\frac{{x}−\mathrm{2}}{\mathrm{1}}=\frac{{y}−\mathrm{4}}{\mathrm{1}} \\ $$$${direction}\:{ratio}\:\left(\mathrm{1},\mathrm{1}\right) \\ $$$${r}=\mathrm{2}{i}+\mathrm{4}{j}+\alpha\left({i}+{j}\right) \\ $$$${l}_{\mathrm{1}} \:\:\:{is}\:\:{r}_{\mathrm{1}} =\mathrm{6}{i}+\mathrm{4}{j}+\lambda\left({i}+{j}\right) \\ $$$$\frac{{x}−\mathrm{6}}{\mathrm{1}}=\frac{{y}−\mathrm{4}}{\mathrm{1}}\:{direction}\:{ratio}\:{of}\:{l}_{\mathrm{1}} {is}\:\left(\mathrm{1},\mathrm{1}\right) \\ $$$${so}\:{AB}\:\:\parallel\:{to}\:{l}_{\mathrm{1}} \\ $$$${l}_{\mathrm{2}} \:{eqn}\:{is}\:\frac{{x}−\mathrm{6}}{\mathrm{6}−\mathrm{4}}=\frac{{z}−\mathrm{0}}{\mathrm{0}−\mathrm{2}} \\ $$$${vector}\:{eqn}\:{l}_{\mathrm{2}} {is}\:\:\:{r}=\mathrm{6}{i}+\mathrm{0}{k}+\lambda\left(\mathrm{2}{i}−\mathrm{2}{k}\right) \\ $$$${or}\:\:\frac{{x}−\mathrm{4}}{\mathrm{6}−\mathrm{4}}=\frac{{z}−\mathrm{2}}{\mathrm{0}−\mathrm{2}}\rightarrow{r}=\mathrm{4}{i}+\mathrm{2}{k}+\lambda\left(\mathrm{2}{i}−\mathrm{2}{k}\right) \\ $$$$ \\ $$
