Question Number 117259 by bemath last updated on 10/Oct/20

Answered by Dwaipayan Shikari last updated on 10/Oct/20
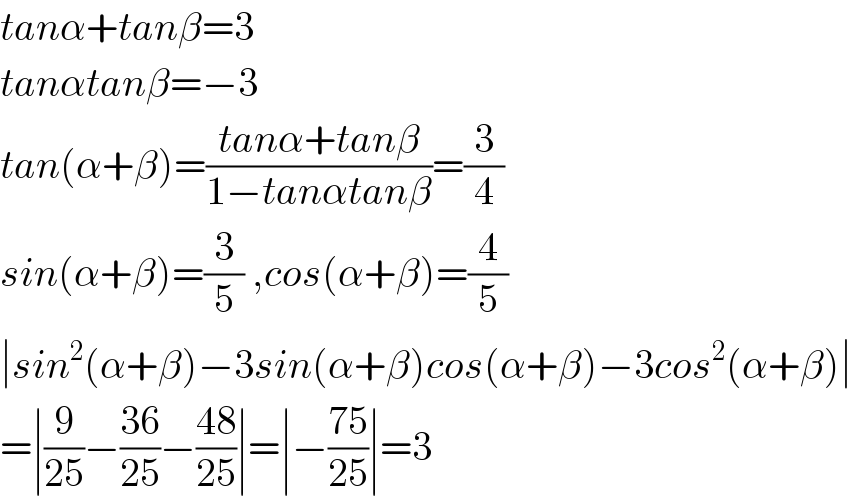
$${tan}\alpha+{tan}\beta=\mathrm{3} \\ $$$${tan}\alpha{tan}\beta=−\mathrm{3} \\ $$$${tan}\left(\alpha+\beta\right)=\frac{{tan}\alpha+{tan}\beta}{\mathrm{1}−{tan}\alpha{tan}\beta}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${sin}\left(\alpha+\beta\right)=\frac{\mathrm{3}}{\mathrm{5}}\:,{cos}\left(\alpha+\beta\right)=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mid{sin}^{\mathrm{2}} \left(\alpha+\beta\right)−\mathrm{3}{sin}\left(\alpha+\beta\right){cos}\left(\alpha+\beta\right)−\mathrm{3}{cos}^{\mathrm{2}} \left(\alpha+\beta\right)\mid \\ $$$$=\mid\frac{\mathrm{9}}{\mathrm{25}}−\frac{\mathrm{36}}{\mathrm{25}}−\frac{\mathrm{48}}{\mathrm{25}}\mid=\mid−\frac{\mathrm{75}}{\mathrm{25}}\mid=\mathrm{3} \\ $$
Commented by bemath last updated on 10/Oct/20

$$\mathrm{santuyyy} \\ $$
Answered by bemath last updated on 10/Oct/20

