Menu Close

Question-117295

Tinku Tara 0 Comments
Pin




Question Number 117295 by mohammad17 last updated on 10/Oct/20
Answered by mr W last updated on 10/Oct/20
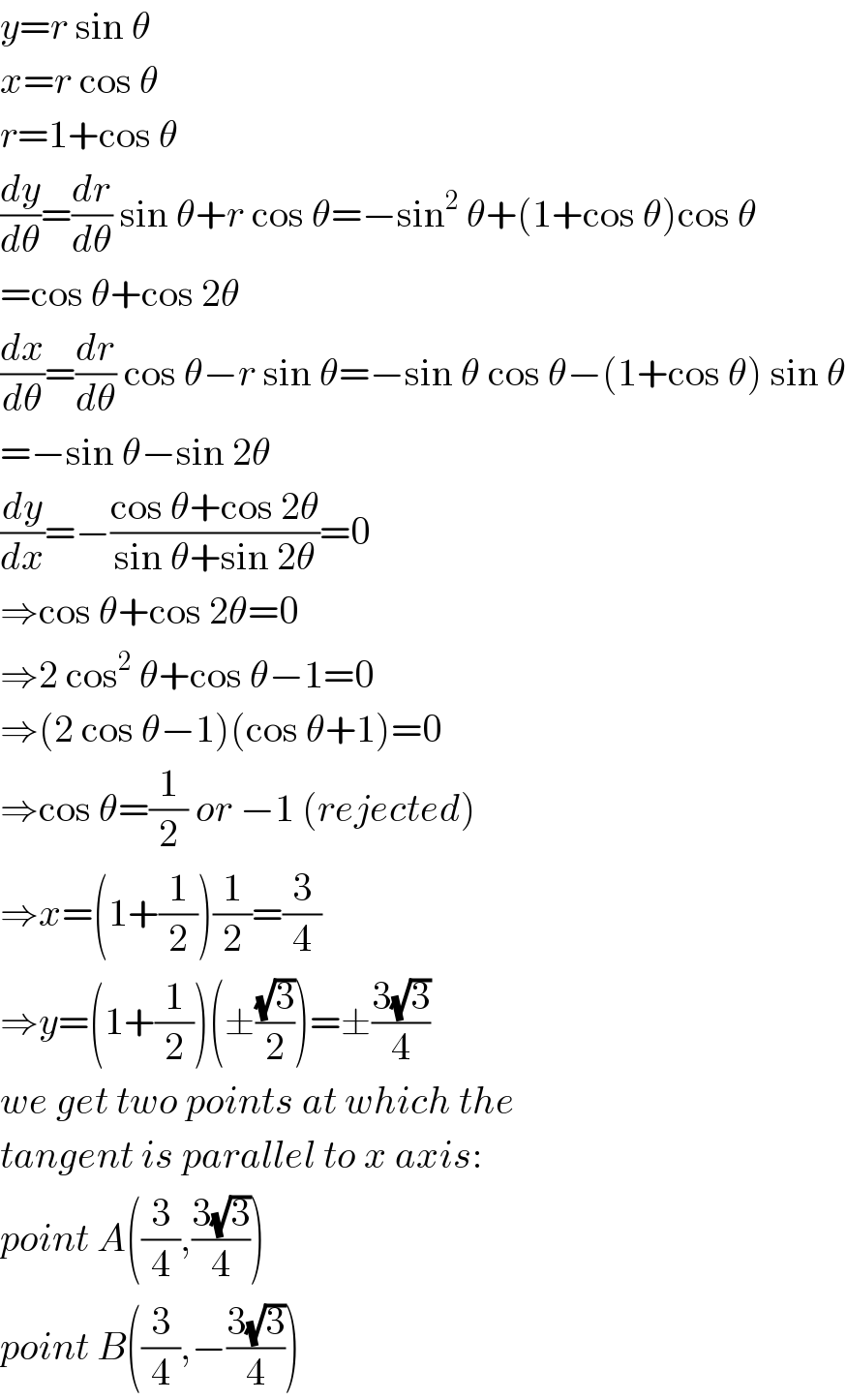
y=r sin θ x=r cos θ r=1+cos θ (dy/dθ)=(dr/dθ) sin θ+r cos θ=−sin^2 θ+(1+cos θ)cos θ =cos θ+cos 2θ (dx/dθ)=(dr/dθ) cos θ−r sin θ=−sin θ cos θ−(1+cos θ) sin θ =−sin θ−sin 2θ (dy/dx)=−((cos θ+cos 2θ)/(sin θ+sin 2θ))=0 ⇒cos θ+cos 2θ=0 ⇒2 cos^2 θ+cos θ−1=0 ⇒(2 cos θ−1)(cos θ+1)=0 ⇒cos θ=(1/2) or −1 (rejected) ⇒x=(1+(1/2))(1/2)=(3/4) ⇒y=(1+(1/2))(±((√3)/2))=±((3(√3))/4) we get two points at which the tangent is parallel to x axis: point A((3/4),((3(√3))/4)) point B((3/4),−((3(√3))/4))
$${y}={r}\:\mathrm{sin}\:\theta \\ $$$${x}={r}\:\mathrm{cos}\:\theta \\ $$$${r}=\mathrm{1}+\mathrm{cos}\:\theta \\ $$$$\frac{{dy}}{{d}\theta}=\frac{{dr}}{{d}\theta}\:\mathrm{sin}\:\theta+{r}\:\mathrm{cos}\:\theta=−\mathrm{sin}^{\mathrm{2}} \:\theta+\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\mathrm{cos}\:\theta \\ $$$$=\mathrm{cos}\:\theta+\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\frac{{dx}}{{d}\theta}=\frac{{dr}}{{d}\theta}\:\mathrm{cos}\:\theta−{r}\:\mathrm{sin}\:\theta=−\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\:\mathrm{sin}\:\theta \\ $$$$=−\mathrm{sin}\:\theta−\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{cos}\:\theta+\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{sin}\:\theta+\mathrm{sin}\:\mathrm{2}\theta}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\theta+\mathrm{cos}\:\mathrm{2}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{cos}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{1}\right)\left(\mathrm{cos}\:\theta+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:−\mathrm{1}\:\left({rejected}\right) \\ $$$$\Rightarrow{x}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{y}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\pm\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$${we}\:{get}\:{two}\:{points}\:{at}\:{which}\:{the} \\ $$$${tangent}\:{is}\:{parallel}\:{to}\:{x}\:{axis}: \\ $$$${point}\:{A}\left(\frac{\mathrm{3}}{\mathrm{4}},\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$${point}\:{B}\left(\frac{\mathrm{3}}{\mathrm{4}},−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$
Commented by mr W last updated on 10/Oct/20
Commented by mohammad17 last updated on 10/Oct/20
tbank you very much sir
$${tbank}\:{you}\:{very}\:{much}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *