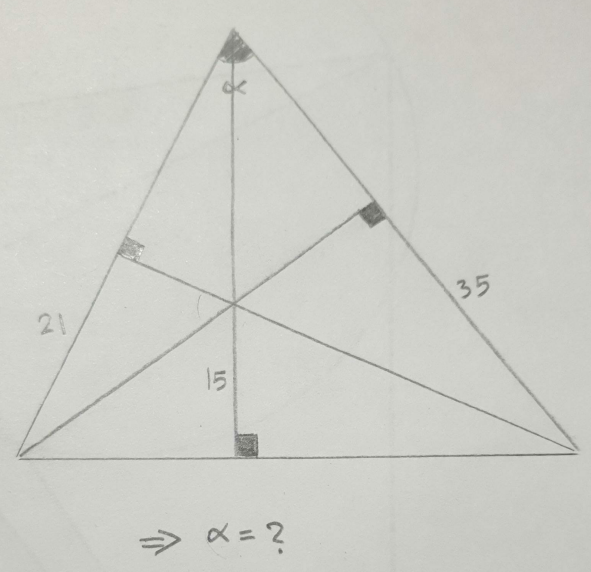
Question Number 117480 by I want to learn more last updated on 12/Oct/20
Commented by Tawa11 last updated on 15/Sep/21

$$\mathrm{nice} \\ $$
Answered by mr W last updated on 12/Oct/20
Commented by mr W last updated on 12/Oct/20
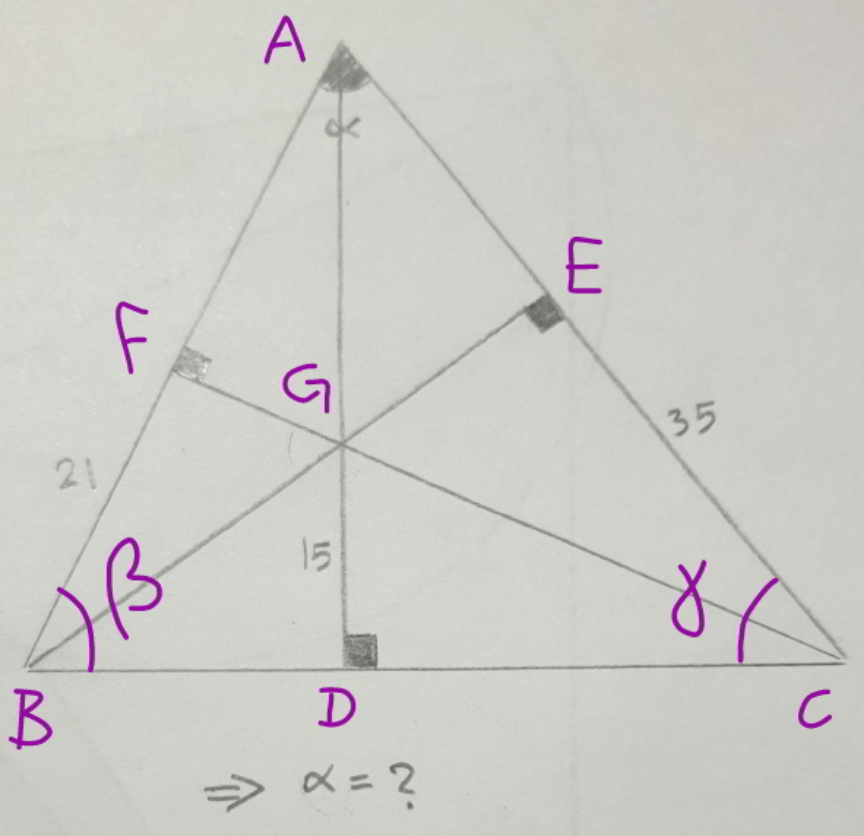
![let BC=a cos β=((21)/a) cos γ=((35)/a) ((AC)/(sin β))=((BC)/(sin (β+γ)))=(a/(sin β cos γ+cos β sin γ)) AC=((a sin β)/(sin β cos γ+cos β sin γ)) DC=AC cos γ=((a sin β cos γ)/(sin β cos γ+cos β sin γ)) DG tan β=DC 15 tan β =((a sin β cos γ)/(sin β cos γ+cos β sin γ)) 15=((a cos β cos γ)/(sin β cos γ+cos β sin γ)) tan β+tan γ=(a/(15)) (√(((a/(21)))^2 −1))+(√(((a/(35)))^2 −1))=(a/(15)) ((a/(21)))^2 −1=((a/(15)))^2 +((a/(35)))^2 −1−2((a/(15)))(√(((a/(35)))^2 −1)) a^2 [(1/(35^2 ))−((1/(15^2 ))+(1/(35^2 ))−(1/(21^2 )))^2 (((15)/2))^2 ]=1 ⇒a=(1/( (√((1/(35^2 ))−((1/(15^2 ))+(1/(35^2 ))−(1/(21^2 )))^2 (((15)/2))^2 ))))=((98)/( (√3))) ⇒β=cos^(−1) ((21)/a)=cos^(−1) ((3(√3))/(14)) ⇒γ=cos^(−1) ((35)/a)=cos^(−1) ((5(√3))/(14)) ⇒α=π−cos^(−1) ((3(√3))/(14))−cos^(−1) ((5(√3))/(14))=(π/3)=60°](https://www.tinkutara.com/question/Q117610.png)
$${let}\:{BC}={a} \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{21}}{{a}} \\ $$$$\mathrm{cos}\:\gamma=\frac{\mathrm{35}}{{a}} \\ $$$$\frac{{AC}}{\mathrm{sin}\:\beta}=\frac{{BC}}{\mathrm{sin}\:\left(\beta+\gamma\right)}=\frac{{a}}{\mathrm{sin}\:\beta\:\mathrm{cos}\:\gamma+\mathrm{cos}\:\beta\:\mathrm{sin}\:\gamma} \\ $$$${AC}=\frac{{a}\:\mathrm{sin}\:\beta}{\mathrm{sin}\:\beta\:\mathrm{cos}\:\gamma+\mathrm{cos}\:\beta\:\mathrm{sin}\:\gamma} \\ $$$${DC}={AC}\:\mathrm{cos}\:\gamma=\frac{{a}\:\mathrm{sin}\:\beta\:\mathrm{cos}\:\gamma}{\mathrm{sin}\:\beta\:\mathrm{cos}\:\gamma+\mathrm{cos}\:\beta\:\mathrm{sin}\:\gamma} \\ $$$${DG}\:\mathrm{tan}\:\beta={DC} \\ $$$$\mathrm{15}\:\mathrm{tan}\:\beta\:=\frac{{a}\:\mathrm{sin}\:\beta\:\mathrm{cos}\:\gamma}{\mathrm{sin}\:\beta\:\mathrm{cos}\:\gamma+\mathrm{cos}\:\beta\:\mathrm{sin}\:\gamma} \\ $$$$\mathrm{15}=\frac{{a}\:\mathrm{cos}\:\beta\:\mathrm{cos}\:\gamma}{\mathrm{sin}\:\beta\:\mathrm{cos}\:\gamma+\mathrm{cos}\:\beta\:\mathrm{sin}\:\gamma} \\ $$$$\mathrm{tan}\:\beta+\mathrm{tan}\:\gamma=\frac{{a}}{\mathrm{15}} \\ $$$$\sqrt{\left(\frac{{a}}{\mathrm{21}}\right)^{\mathrm{2}} −\mathrm{1}}+\sqrt{\left(\frac{{a}}{\mathrm{35}}\right)^{\mathrm{2}} −\mathrm{1}}=\frac{{a}}{\mathrm{15}} \\ $$$$\left(\frac{{a}}{\mathrm{21}}\right)^{\mathrm{2}} −\mathrm{1}=\left(\frac{{a}}{\mathrm{15}}\right)^{\mathrm{2}} +\left(\frac{{a}}{\mathrm{35}}\right)^{\mathrm{2}} −\mathrm{1}−\mathrm{2}\left(\frac{{a}}{\mathrm{15}}\right)\sqrt{\left(\frac{{a}}{\mathrm{35}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$${a}^{\mathrm{2}} \left[\frac{\mathrm{1}}{\mathrm{35}^{\mathrm{2}} }−\left(\frac{\mathrm{1}}{\mathrm{15}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{35}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{21}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{\mathrm{15}}{\mathrm{2}}\right)^{\mathrm{2}} \right]=\mathrm{1} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{35}^{\mathrm{2}} }−\left(\frac{\mathrm{1}}{\mathrm{15}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{35}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{21}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{\mathrm{15}}{\mathrm{2}}\right)^{\mathrm{2}} }}=\frac{\mathrm{98}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\beta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{21}}{{a}}=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{14}} \\ $$$$\Rightarrow\gamma=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{35}}{{a}}=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{14}} \\ $$$$\Rightarrow\alpha=\pi−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{14}}−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{14}}=\frac{\pi}{\mathrm{3}}=\mathrm{60}° \\ $$
Commented by I want to learn more last updated on 12/Oct/20

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
