Menu Close

Question-117481

Tinku Tara 0 Comments
Pin




Question Number 117481 by I want to learn more last updated on 12/Oct/20
Answered by mr W last updated on 12/Oct/20
let AC=1 ((OC)/(sin 20))=((AC)/(sin (10+20))) ⇒OC=((sin 20)/(sin 30))=2 sin 20 ((BC)/(sin 40))=((AC)/(sin (30+10+20+20))) ⇒BC=(1/(2 cos 40)) ((BC)/(sin (x+30)))=((OC)/(sin x)) ((sin (x+30))/(sin x))=((BC)/(OC))=(1/(4 cos 40 sin 20)) cos 30+((sin 30)/(tan x))=(1/(4 cos 40 sin 20)) (1/(tan x))=((1/(2 cos 40 sin 20))−(√3)) ⇒x=80°
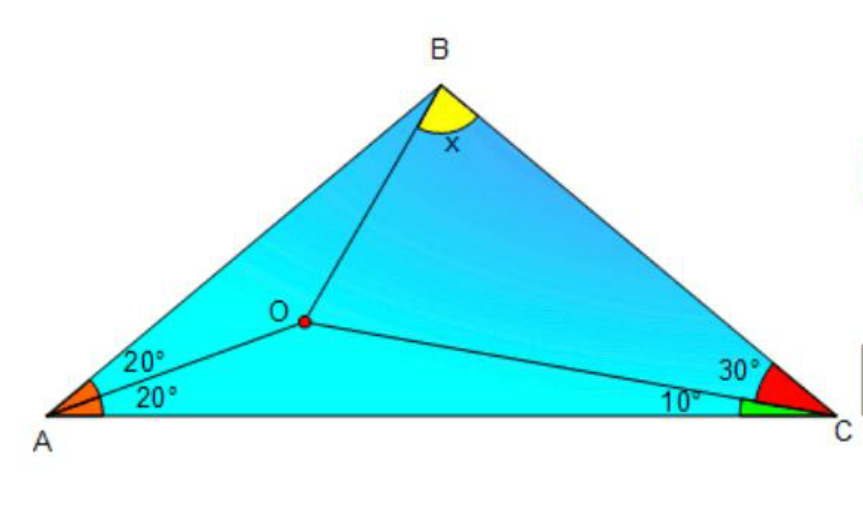
$${let}\:{AC}=\mathrm{1} \\ $$$$\frac{{OC}}{\mathrm{sin}\:\mathrm{20}}=\frac{{AC}}{\mathrm{sin}\:\left(\mathrm{10}+\mathrm{20}\right)} \\ $$$$\Rightarrow{OC}=\frac{\mathrm{sin}\:\mathrm{20}}{\mathrm{sin}\:\mathrm{30}}=\mathrm{2}\:\mathrm{sin}\:\mathrm{20} \\ $$$$\frac{{BC}}{\mathrm{sin}\:\mathrm{40}}=\frac{{AC}}{\mathrm{sin}\:\left(\mathrm{30}+\mathrm{10}+\mathrm{20}+\mathrm{20}\right)} \\ $$$$\Rightarrow{BC}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}} \\ $$$$\frac{{BC}}{\mathrm{sin}\:\left({x}+\mathrm{30}\right)}=\frac{{OC}}{\mathrm{sin}\:{x}} \\ $$$$\frac{\mathrm{sin}\:\left({x}+\mathrm{30}\right)}{\mathrm{sin}\:{x}}=\frac{{BC}}{{OC}}=\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{cos}\:\mathrm{40}\:\mathrm{sin}\:\mathrm{20}} \\ $$$$\mathrm{cos}\:\mathrm{30}+\frac{\mathrm{sin}\:\mathrm{30}}{\mathrm{tan}\:{x}}=\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{cos}\:\mathrm{40}\:\mathrm{sin}\:\mathrm{20}} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:{x}}=\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}\:\mathrm{sin}\:\mathrm{20}}−\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow{x}=\mathrm{80}° \\ $$
Commented by I want to learn more last updated on 12/Oct/20
Thanks sir. I appreciate
$$\mathrm{T}{hanks}\:{sir}.\:{I}\:{appreciate} \\ $$
Commented by I want to learn more last updated on 12/Oct/20
sir, please help with Q117480
$$\mathrm{sir},\:\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\:\mathrm{Q117480} \\ $$
Answered by 1549442205PVT last updated on 12/Oct/20
Commented by 1549442205PVT last updated on 12/Oct/20
Construct the equilateral triangle BCD such that D lie on halfplane with the edge being the line AC don′t containing B.Then BCD^(�) =BDC^(�) =CBD^(�) =60°.From the hypothesis BAC^(�) =BCA^(�) =40°we get ACD^(�) =20°,ABD^(�) =100°−60°=40° BA=BD=BC=CD⇒ΔABD is isosceles at B⇒BAD^(�) =BDA^(�) =70° ⇒CAD^(�) =70°−40°=30°(∗) Draw the ray Cx such that BCx ^(�) =30° M=(AB)∩Cx.ThenAMC^(�) =180°−(40+70) =70°.Suppose O′ is the point symetry to M through BC,E=BC∩MO′then BME^(�) =BMC^(�) −CME^(�) =70−60=10° ⇒CBM^(�) =80°= CBO′^(�) (the property of two symetric figures).We will prove that O≡O′.Indeed,we have ABO^(�) = ABC^(�) −CBO′^(�) =100−80=20°=(1/2)ABD^(�) O′∈CO since BCO^(�) =BCO′^(�) =30° CO′D^(�) =CO′B^(�) =70°and CDO′^(�) =CBO′^(�) =80° (since CO′Dand CO′B are two symetric figures through CO)⇒O′DA^(�) =ADC^(�) −CDO′^(�) =130−80=50°.(1) ΔBO′A=ΔBO′D(s.a.s)⇒BO′A^(�) =BO′D^(�) =140°⇒AO′D^(�) =360−2.140=80°(2) From (1)(2)we get O′AD^(�) =180−(50+80) =50°⇒O′AC^(�) =50−30=20°=OAC^(�) (3) but O′CA^(�) =10°(4).From(3)(4)we infer O′≡O.That shows that x=CBO^(�) =80°
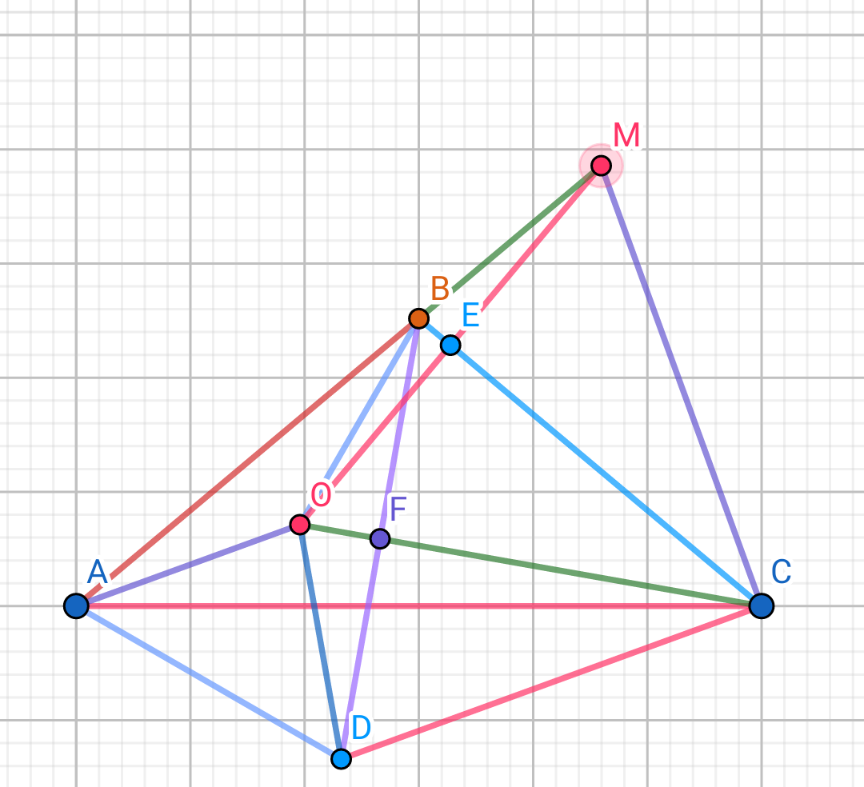
$$\mathrm{Construct}\:\mathrm{the}\:\mathrm{equilateral}\:\mathrm{triangle} \\ $$$$\mathrm{BCD}\:\mathrm{such}\:\mathrm{that}\:\mathrm{D}\:\mathrm{lie}\:\mathrm{on}\:\mathrm{halfplane} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{edge}\:\mathrm{being}\:\mathrm{the}\:\mathrm{line}\:\:\mathrm{AC}\:\:\mathrm{don}'\mathrm{t} \\ $$$$\mathrm{containing}\:\mathrm{B}.\mathrm{Then} \\ $$$$\widehat {\mathrm{BCD}}=\widehat {\mathrm{BDC}}=\widehat {\mathrm{CBD}}=\mathrm{60}°.\mathrm{From}\:\mathrm{the} \\ $$$$\mathrm{hypothesis}\:\widehat {\mathrm{BAC}}=\widehat {\mathrm{BCA}}=\mathrm{40}°\mathrm{we}\:\mathrm{get} \\ $$$$\widehat {\mathrm{ACD}}=\mathrm{20}°,\widehat {\mathrm{ABD}}=\mathrm{100}°−\mathrm{60}°=\mathrm{40}° \\ $$$$\mathrm{BA}=\mathrm{BD}=\mathrm{BC}=\mathrm{CD}\Rightarrow\Delta\mathrm{ABD}\:\mathrm{is} \\ $$$$\mathrm{isosceles}\:\mathrm{at}\:\mathrm{B}\Rightarrow\widehat {\mathrm{BAD}}=\widehat {\mathrm{BDA}}=\mathrm{70}° \\ $$$$\Rightarrow\widehat {\mathrm{CAD}}=\mathrm{70}°−\mathrm{40}°=\mathrm{30}°\left(\ast\right) \\ $$$$\mathrm{Draw}\:\mathrm{the}\:\mathrm{ray}\:\mathrm{Cx}\:\mathrm{such}\:\mathrm{that}\widehat {\:\mathrm{BCx}\:}=\mathrm{30}° \\ $$$$\mathrm{M}=\left(\mathrm{AB}\right)\cap\mathrm{Cx}.\mathrm{Then}\widehat {\mathrm{AMC}}=\mathrm{180}°−\left(\mathrm{40}+\mathrm{70}\right) \\ $$$$=\mathrm{70}°.\mathrm{Suppose}\:\mathrm{O}'\:\mathrm{is}\:\mathrm{the}\:\mathrm{point}\:\mathrm{symetry} \\ $$$$\mathrm{to}\:\mathrm{M}\:\mathrm{through}\:\mathrm{BC},\mathrm{E}=\mathrm{BC}\cap\mathrm{MO}'\mathrm{then} \\ $$$$\widehat {\mathrm{BME}}=\widehat {\mathrm{BMC}}−\widehat {\mathrm{CME}}=\mathrm{70}−\mathrm{60}=\mathrm{10}° \\ $$$$\Rightarrow\widehat {\mathrm{CBM}}=\mathrm{80}°=\:\widehat {\mathrm{CBO}'}\left(\mathrm{the}\:\mathrm{property}\:\mathrm{of}\right. \\ $$$$\left.\mathrm{two}\:\mathrm{symetric}\:\mathrm{figures}\right).\mathrm{We}\:\mathrm{will}\:\mathrm{prove} \\ $$$$\mathrm{that}\:\mathrm{O}\equiv\mathrm{O}'.\mathrm{Indeed},\mathrm{we}\:\mathrm{have}\:\widehat {\mathrm{ABO}}= \\ $$$$\widehat {\mathrm{ABC}}−\widehat {\mathrm{CBO}'}=\mathrm{100}−\mathrm{80}=\mathrm{20}°=\frac{\mathrm{1}}{\mathrm{2}}\widehat {\mathrm{ABD}} \\ $$$$\mathrm{O}'\in\mathrm{CO}\:\mathrm{since}\:\widehat {\mathrm{BCO}}=\widehat {\mathrm{BCO}'}=\mathrm{30}° \\ $$$$\widehat {\mathrm{CO}'\mathrm{D}}=\widehat {\mathrm{CO}'\mathrm{B}}=\mathrm{70}°\mathrm{and}\:\widehat {\mathrm{CDO}'}=\widehat {\mathrm{CBO}'}=\mathrm{80}° \\ $$$$\left(\mathrm{since}\:\mathrm{CO}'\mathrm{Dand}\:\mathrm{CO}'\mathrm{B}\:\mathrm{are}\:\mathrm{two}\:\mathrm{symetric}\right. \\ $$$$\left.\mathrm{figures}\:\mathrm{through}\:\mathrm{CO}\right)\Rightarrow\widehat {\mathrm{O}'\mathrm{DA}}=\widehat {\mathrm{ADC}} \\ $$$$−\widehat {\mathrm{CDO}'}=\mathrm{130}−\mathrm{80}=\mathrm{50}°.\left(\mathrm{1}\right) \\ $$$$\Delta\mathrm{BO}'\mathrm{A}=\Delta\mathrm{BO}'\mathrm{D}\left(\mathrm{s}.\mathrm{a}.\mathrm{s}\right)\Rightarrow\widehat {\mathrm{BO}'\mathrm{A}}=\widehat {\mathrm{BO}'\mathrm{D}} \\ $$$$=\mathrm{140}°\Rightarrow\widehat {\mathrm{AO}'\mathrm{D}}=\mathrm{360}−\mathrm{2}.\mathrm{140}=\mathrm{80}°\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get}\:\widehat {\mathrm{O}'\mathrm{AD}}=\mathrm{180}−\left(\mathrm{50}+\mathrm{80}\right) \\ $$$$=\mathrm{50}°\Rightarrow\widehat {\mathrm{O}'\mathrm{AC}}=\mathrm{50}−\mathrm{30}=\mathrm{20}°=\widehat {\mathrm{OAC}}\left(\mathrm{3}\right) \\ $$$$\mathrm{but}\:\widehat {\mathrm{O}'\mathrm{CA}}=\mathrm{10}°\left(\mathrm{4}\right).\mathrm{From}\left(\mathrm{3}\right)\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{infer} \\ $$$$\mathrm{O}'\equiv\mathrm{O}.\mathrm{That}\:\mathrm{shows}\:\mathrm{that}\:\mathrm{x}=\widehat {\mathrm{CBO}}=\mathrm{80}° \\ $$
Commented by I want to learn more last updated on 12/Oct/20
Thanks sir, i appreciate.
$${Thanks}\:{sir},\:{i}\:{appreciate}. \\ $$
Commented by I want to learn more last updated on 12/Oct/20
sir, please help with Q117480
$$\mathrm{sir},\:\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\:\mathrm{Q117480} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *