Question Number 117646 by bemath last updated on 13/Oct/20
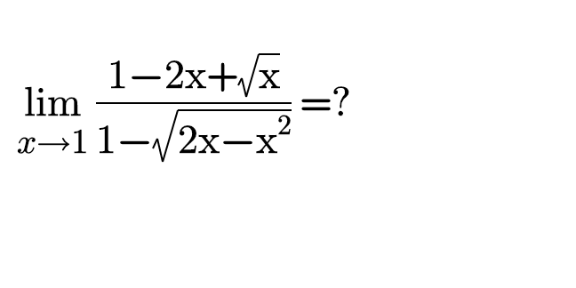
Commented by bemath last updated on 13/Oct/20
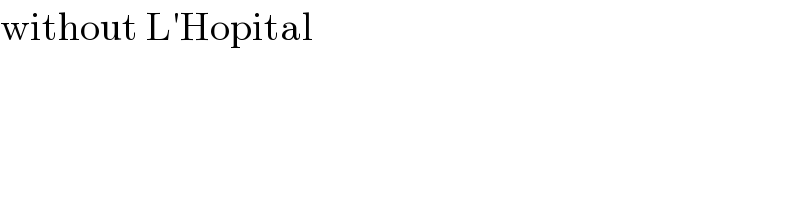
$$\mathrm{without}\:\mathrm{L}'\mathrm{Hopital} \\ $$
Answered by bobhans last updated on 13/Oct/20
![lim_(x→1) [((1−2x+(√x))/(1−(√(2x−x^2 )))) ]×((1+(√(2x−x^2 )))/(1+(√(2x−x^2 )))) = 2 ×lim_(x→1) (((1+(√x))−2x)/(x^2 −2x+1)) = 2×lim_(x→1) (((1+(√x))−2x)/((x−1)^2 )) 2×lim_(x→1) (((1+(√x))−2x)/(((√x)+1)^2 ((√x)−1)^2 )) = (1/2)×lim_(x→1) (((1+(√x))−2x)/(((√x)−1)^2 )) −(1/2)×lim_(x→1) ((2((√x))^2 −(√x)−1)/(((√x)−1)^2 )) = −(1/2)×lim_(x→1) (((2(√x) +1)((√x)−1))/(((√x)−1)^2 )) = −(1/2) lim_(x→1) ((2(√x)+1)/( (√x)−1)) = ±∞ or doesnot exist](https://www.tinkutara.com/question/Q117656.png)
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left[\frac{\mathrm{1}−\mathrm{2x}+\sqrt{\mathrm{x}}}{\mathrm{1}−\sqrt{\mathrm{2x}−\mathrm{x}^{\mathrm{2}} }}\:\right]×\frac{\mathrm{1}+\sqrt{\mathrm{2x}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{1}+\sqrt{\mathrm{2x}−\mathrm{x}^{\mathrm{2}} }}\:= \\ $$$$\mathrm{2}\:×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{x}}\right)−\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}\:=\:\mathrm{2}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{x}}\right)−\mathrm{2x}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{x}}\right)−\mathrm{2x}}{\left(\sqrt{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{2}} \left(\sqrt{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\sqrt{\mathrm{x}}\right)−\mathrm{2x}}{\left(\sqrt{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\sqrt{\mathrm{x}}\right)^{\mathrm{2}} −\sqrt{\mathrm{x}}−\mathrm{1}}{\left(\sqrt{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:= \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\mathrm{2}\sqrt{\mathrm{x}}\:+\mathrm{1}\right)\left(\sqrt{\mathrm{x}}−\mathrm{1}\right)}{\left(\sqrt{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:= \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\:\sqrt{\mathrm{x}}−\mathrm{1}}\:=\:\pm\infty\:\mathrm{or}\:\mathrm{doesnot}\:\mathrm{exist} \\ $$
Answered by MJS_new last updated on 13/Oct/20
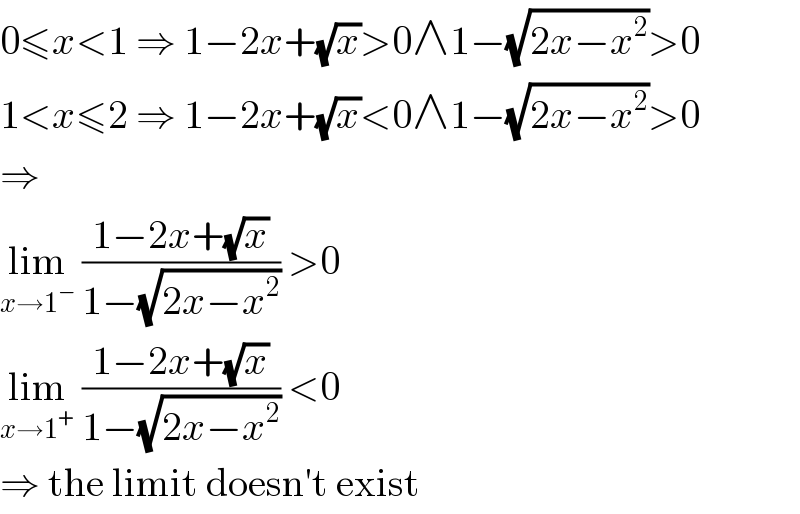
$$\mathrm{0}\leqslant{x}<\mathrm{1}\:\Rightarrow\:\mathrm{1}−\mathrm{2}{x}+\sqrt{{x}}>\mathrm{0}\wedge\mathrm{1}−\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }>\mathrm{0} \\ $$$$\mathrm{1}<{x}\leqslant\mathrm{2}\:\Rightarrow\:\mathrm{1}−\mathrm{2}{x}+\sqrt{{x}}<\mathrm{0}\wedge\mathrm{1}−\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }>\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{2}{x}+\sqrt{{x}}}{\mathrm{1}−\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}\:>\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{2}{x}+\sqrt{{x}}}{\mathrm{1}−\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}\:<\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$
Commented by bemath last updated on 13/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
