Question-117673

Question Number 117673 by huotpat last updated on 13/Oct/20

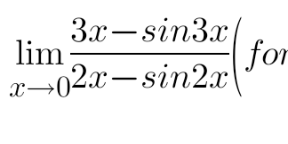
Answered by bemath last updated on 13/Oct/20

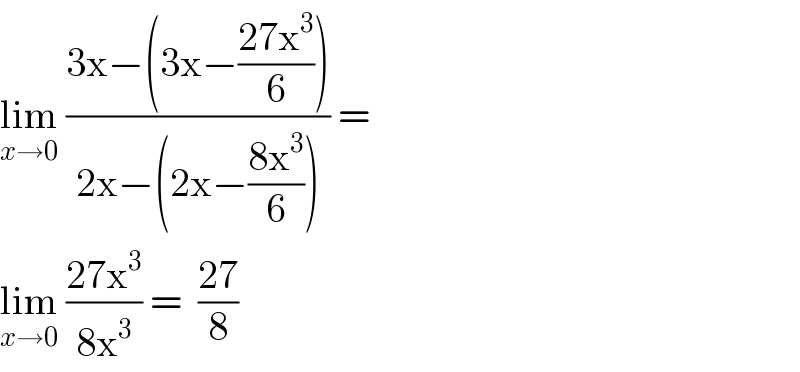
lim_(x→0) ((3x−(3x−((27x^3 )/6)))/(2x−(2x−((8x^3 )/6)))) = lim_(x→0) ((27x^3 )/(8x^3 )) = ((27)/8)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3x}−\left(\mathrm{3x}−\frac{\mathrm{27x}^{\mathrm{3}} }{\mathrm{6}}\right)}{\mathrm{2x}−\left(\mathrm{2x}−\frac{\mathrm{8x}^{\mathrm{3}} }{\mathrm{6}}\right)}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{27x}^{\mathrm{3}} }{\mathrm{8x}^{\mathrm{3}} }\:=\:\:\frac{\mathrm{27}}{\mathrm{8}} \\ $$

Commented by MJS_new last updated on 13/Oct/20

$$\mathrm{typo}:\:\mathrm{it}'\mathrm{s}\:\frac{\mathrm{27}{x}^{\mathrm{3}} }{\mathrm{8}{x}^{\mathrm{3}} } \\ $$

Commented by bemath last updated on 13/Oct/20

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{thank}\:\mathrm{you} \\ $$

Answered by Olaf last updated on 13/Oct/20

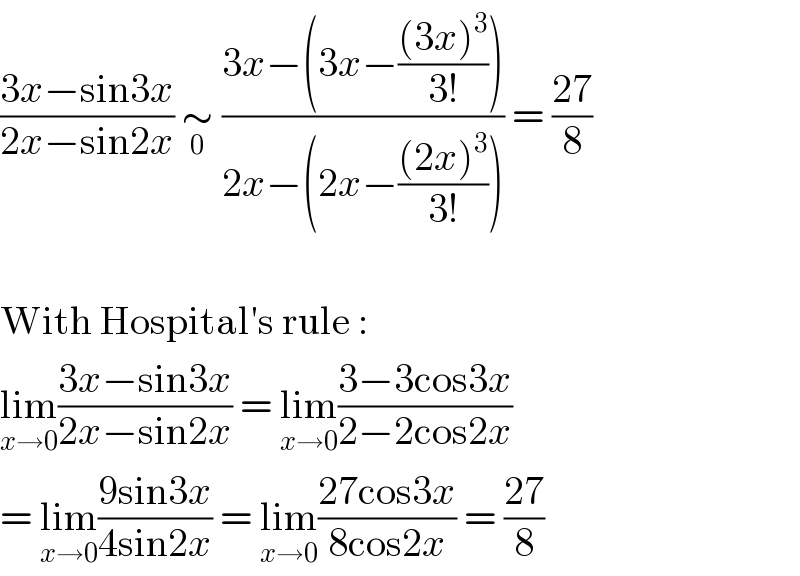
((3x−sin3x)/(2x−sin2x)) ∼_0 ((3x−(3x−(((3x)^3 )/(3!))))/(2x−(2x−(((2x)^3 )/(3!))))) = ((27)/8) With Hospital′s rule : lim_(x→0) ((3x−sin3x)/(2x−sin2x)) = lim_(x→0) ((3−3cos3x)/(2−2cos2x)) = lim_(x→0) ((9sin3x)/(4sin2x)) = lim_(x→0) ((27cos3x)/(8cos2x)) = ((27)/8)

$$\frac{\mathrm{3}{x}−\mathrm{sin3}{x}}{\mathrm{2}{x}−\mathrm{sin2}{x}}\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{3}{x}−\left(\mathrm{3}{x}−\frac{\left(\mathrm{3}{x}\right)^{\mathrm{3}} }{\mathrm{3}!}\right)}{\mathrm{2}{x}−\left(\mathrm{2}{x}−\frac{\left(\mathrm{2}{x}\right)^{\mathrm{3}} }{\mathrm{3}!}\right)}\:=\:\frac{\mathrm{27}}{\mathrm{8}} \\ $$$$ \\ $$$$\mathrm{With}\:\mathrm{Hospital}'\mathrm{s}\:\mathrm{rule}\:: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{x}−\mathrm{sin3}{x}}{\mathrm{2}{x}−\mathrm{sin2}{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}−\mathrm{3cos3}{x}}{\mathrm{2}−\mathrm{2cos2}{x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{9sin3}{x}}{\mathrm{4sin2}{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{27cos3}{x}}{\mathrm{8cos2}{x}}\:=\:\frac{\mathrm{27}}{\mathrm{8}} \\ $$

Answered by Dwaipayan Shikari last updated on 13/Oct/20

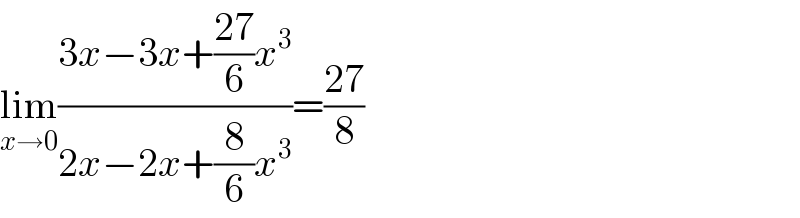
lim_(x→0) ((3x−3x+((27)/6)x^3 )/(2x−2x+(8/6)x^3 ))=((27)/8)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{x}−\mathrm{3}{x}+\frac{\mathrm{27}}{\mathrm{6}}{x}^{\mathrm{3}} }{\mathrm{2}{x}−\mathrm{2}{x}+\frac{\mathrm{8}}{\mathrm{6}}{x}^{\mathrm{3}} }=\frac{\mathrm{27}}{\mathrm{8}} \\ $$

Answered by 1549442205PVT last updated on 13/Oct/20

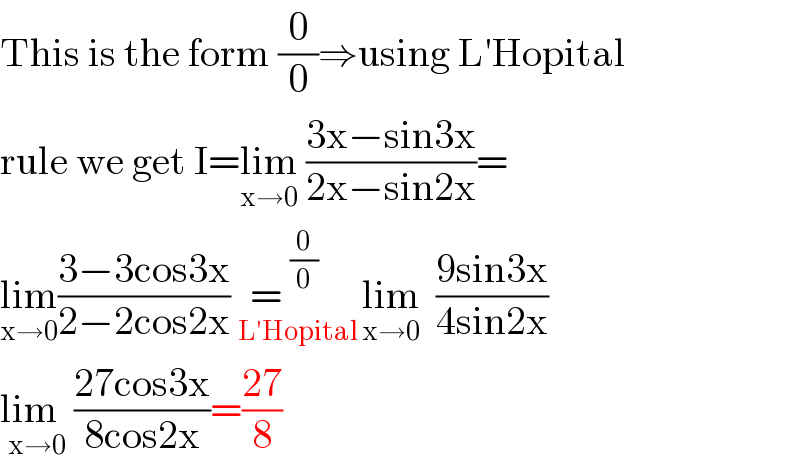
This is the form (0/0)⇒using L′Hopital rule we get I=lim_(x→0) ((3x−sin3x)/(2x−sin2x))= lim_(x→0) ((3−3cos3x)/(2−2cos2x))=^(0/0) _( L′Hopital ) lim_(x→0) ((9sin3x)/(4sin2x)) lim _(x→0) ((27cos3x)/(8cos2x))=((27)/8)

$$\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{form}\:\frac{\mathrm{0}}{\mathrm{0}}\Rightarrow\mathrm{using}\:\mathrm{L}'\mathrm{Hopital} \\ $$$$\mathrm{rule}\:\mathrm{we}\:\mathrm{get}\:\mathrm{I}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3x}−\mathrm{sin3x}}{\mathrm{2x}−\mathrm{sin2x}}= \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}−\mathrm{3cos3x}}{\mathrm{2}−\mathrm{2cos2x}}\underset{\:\:\mathrm{L}'\mathrm{Hopital}\:} {=\:^{\frac{\mathrm{0}}{\mathrm{0}}} \:\:\:}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{9sin3x}}{\mathrm{4sin2x}} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}\:\:}\frac{\mathrm{27cos3x}}{\mathrm{8cos2x}}=\frac{\mathrm{27}}{\mathrm{8}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply