Question Number 117688 by Khalmohmmad last updated on 13/Oct/20
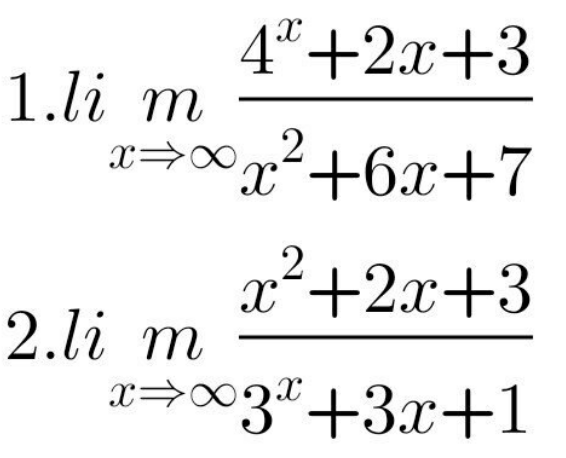
Commented by prakash jain last updated on 13/Oct/20

$$\mathrm{1}.\:\:\frac{{exponential}}{{polynomial}} \\ $$$$\mathrm{2}.\:\frac{{polynomial}}{{exponential}} \\ $$
Commented by Khalmohmmad last updated on 13/Oct/20
$$\mathrm{with}\:\mathrm{is}\:\mathrm{the}\:\mathrm{Answer} \\ $$
Commented by JDamian last updated on 13/Oct/20
You should know that, when base is greater than 1, the exponential function always wins any polynomial.
Answered by 1549442205PVT last updated on 13/Oct/20
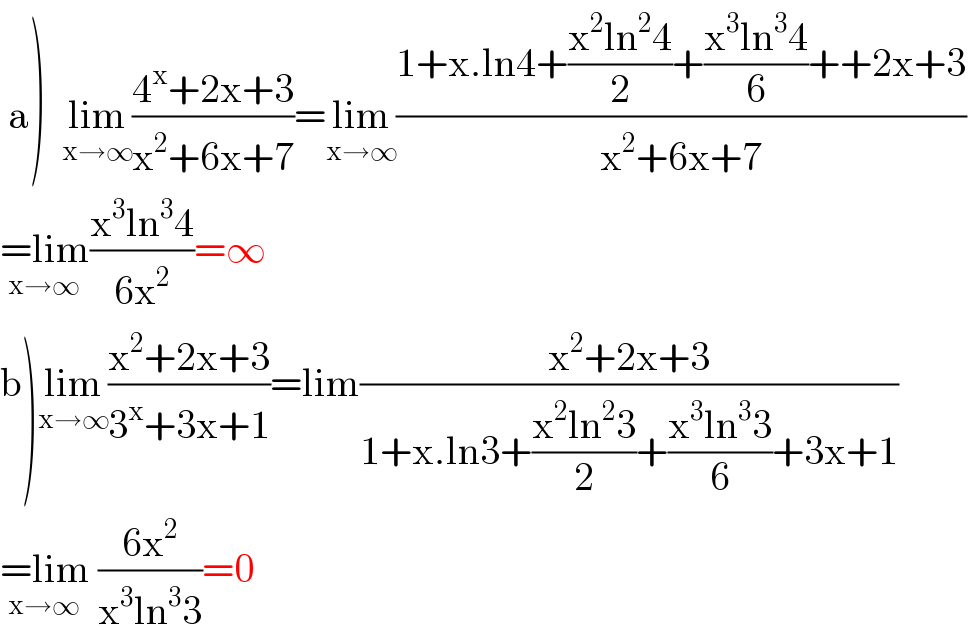
$$\left.\:\mathrm{a}\right)\:\:\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{4}^{\mathrm{x}} +\mathrm{2x}+\mathrm{3}}{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{7}}=\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}+\mathrm{x}.\mathrm{ln4}+\frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}^{\mathrm{2}} \mathrm{4}}{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{3}} \mathrm{ln}^{\mathrm{3}} \mathrm{4}}{\mathrm{6}}++\mathrm{2x}+\mathrm{3}}{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{7}} \\ $$$$\underset{\mathrm{x}\rightarrow\infty} {=\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{3}} \mathrm{ln}^{\mathrm{3}} \mathrm{4}}{\mathrm{6x}^{\mathrm{2}} }=\infty \\ $$$$\left.\mathrm{b}\right)\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{3}}{\mathrm{3}^{\mathrm{x}} +\mathrm{3x}+\mathrm{1}}=\mathrm{lim}\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{3}}{\mathrm{1}+\mathrm{x}.\mathrm{ln3}+\frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}^{\mathrm{2}} \mathrm{3}}{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{3}} \mathrm{ln}^{\mathrm{3}} \mathrm{3}}{\mathrm{6}}+\mathrm{3x}+\mathrm{1}} \\ $$$$\underset{\mathrm{x}\rightarrow\infty} {=\mathrm{lim}}\:\frac{\mathrm{6x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{3}} \mathrm{ln}^{\mathrm{3}} \mathrm{3}}=\mathrm{0} \\ $$
